Question: (a) Well-behaved functions u and 'v are defined on the interval [(1, b], where they obey u(a) = 4, u(b) = 7; 0(a) = 6,
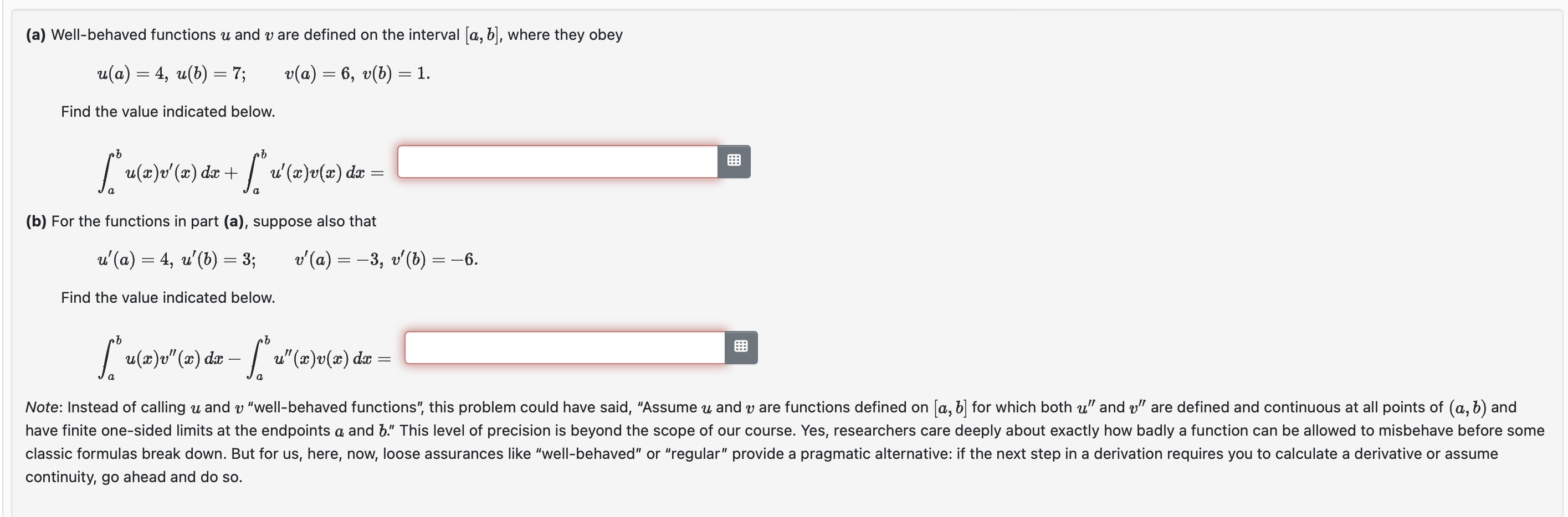
![[(1, b], where they obey u(a) = 4, u(b) = 7; 0(a)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66669e023e49f_15466669e02223f2.jpg)
(a) Well-behaved functions u and 'v are defined on the interval [(1, b], where they obey u(a) = 4, u(b) = 7; 0(a) = 6, 12(1)) = 1. Find the value indicated below. /b u(:b)v'(w) d2: + fbu'(m)v(w) dw = (b) For the functions in part (a), suppose also that u'(a) : 4, u'(b) : 3; u'( 7 3, v'(b) : 6. Find the value indicated below. [EM/lamb fawn\": Note: Instead of calling u and 1; "wellbehaved functions", this problem could have said, "Assume u and v are functions defined on [11, b] for which both 11,\" and v" are defined and continuous at all points of (11., b) and have finite one-sided limits at the endpoints a. and b." This level of precision is beyond the scope of our course, Yes, researchers care deeply about exactly how badly a function can be allowed to misbehave before some classic formulas break down But for us, here, now, loose assurances like "wellbehaved" or "regular" provide a pragmatic alternative: if the next step in a derivation requires you to calculate a derivative or assume continuity, go ahead and do so
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


