A widget inspector inspects 12 widgets and finds that exactly 3 are defective. Unfortunately, the widgets then get all mixed up and the inspector has to find the 3 defective

widgets again by testing widgets one by one.

(a) Find the probability that the inspector will now have to test at least 9 widgets.

(b) Find the probability that the inspector will now have to test at least 10 widgets.

57. There are 15 chocolate bars and 10 children. In how many ways can the chocolate bars

be distributed to the children, in each of the following scenarios?

(a) The chocolate bars are fungible (interchangeable).

(b) The chocolate bars are fungible, and each child must receive at least one.

Hint: First give each child a chocolate bar, and then decide what to do with the rest.

(c) The chocolate bars are not fungible (it matters which particular bar goes where).

(d) The chocolate bars are not fungible, and each child must receive at least one.

Hint: The strategy suggested in (b) does not apply. Instead, consider randomly giving

the chocolate bars to the children, and apply inclusion-exclusion.

7. Two chess players, A and B, are going to play 7 games. Each game has three possible

outcomes: a win for A (which is a loss for B), a draw (tie), and a loss for A (which is

a win for B). A win is worth 1 point, a draw is worth 0.5 points, and a loss is worth 0

points.

(a) How many possible outcomes for the individual games are there, such that overall

player A ends up with 3 wins, 2 draws, and 2 losses?

(b) How many possible outcomes for the individual games are there, such that A ends

up with 4 points and B ends up with 3 points?

(c) Now assume that they are playing a best-of-7 match, where the match will end as

soon as either player has 4 points. For example, if after 6 games the score is 4 to 2 in

favor of A, then A wins the match and they don't play a 7th game. How many possible

outcomes for the individual games are there, such that the match lasts for 7 games and

A wins by a score of 4 to 3?

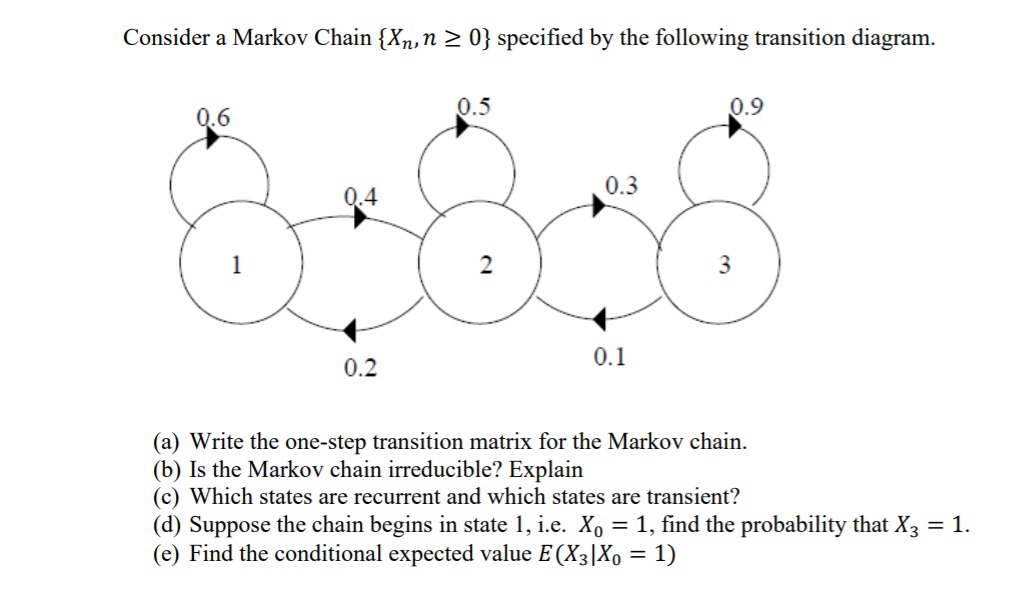
For each of the following transition matrices, do the following. First specify the classes of the following Markov chains and determine whether they are transient or recurrent. Second, determine whether the Markov chain is irreducible or not. Third, if the matrix is irreducible, find the stationary distribution x. Fourth, if the Markov chain is irreducible, determine whether the Markov chain is periodic or not, and give the period. Fifth, for irreducible Markov chains, calculate the expected number of steps to return to each state when starting from the state in the long-run. Finally, using the software, find P109 approximately and check if each row matches with a for irreducible Markov chains. O 0 0 0 P = 1/2 1/2 0 0Problem 6. Below is the transition probability matrix of a Markov chain (X.) with six states. Determine the communication classes of this Markov chain, and determine for each class whether it is recurrent or transient. Is this Markov chain ergodic? Why or why not? 0.9 O 0.2 0.2 04 0 0 0 05 0 0.5 0Consider a Markov Chain {Xn, n 2 0} specified by the following transition diagram. 0.6 0.5 0.9 0.4 0.3 N 0.2 0.1 (a) Write the one-step transition matrix for the Markov chain. (b) Is the Markov chain irreducible? Explain (c) Which states are recurrent and which states are transient? (d) Suppose the chain begins in state 1, i.e. Xo = 1, find the probability that X3 = 1. (e) Find the conditional expected value E (X3|Xo = 1)1. (a) Define the Markov property of a discrete Markov chain. [5 marks] (b) Explain the difference between a homogeneous and inhomoge- neous Markov chain. [5 marks] (c) A three-state Markov chain has transition probability matrix, P, given below 1 2 3 1/ 0.8 0.1 0.1\\ P -2 0.15 0.75 0.1 3 0.06 0.04 0.9 If for all large n /0.3 0.2 0.5 0.3 0.2 0.5 0.3 0.2 0.5 what is the long-term proportion of time the chain spends in each of the three states? [5 marks) (d) State, with proof, whether the Markov chain in the previous ques- tion is reversible. [5 marks] (e) Assume that rows 1, 2 and 3 in the transition probability matrix, P correspond to transitions from states r, s and q, respectively of the chain. If the chain is in state q at some point i, what is the probability it was in state r at point i - 2? [5 marks]