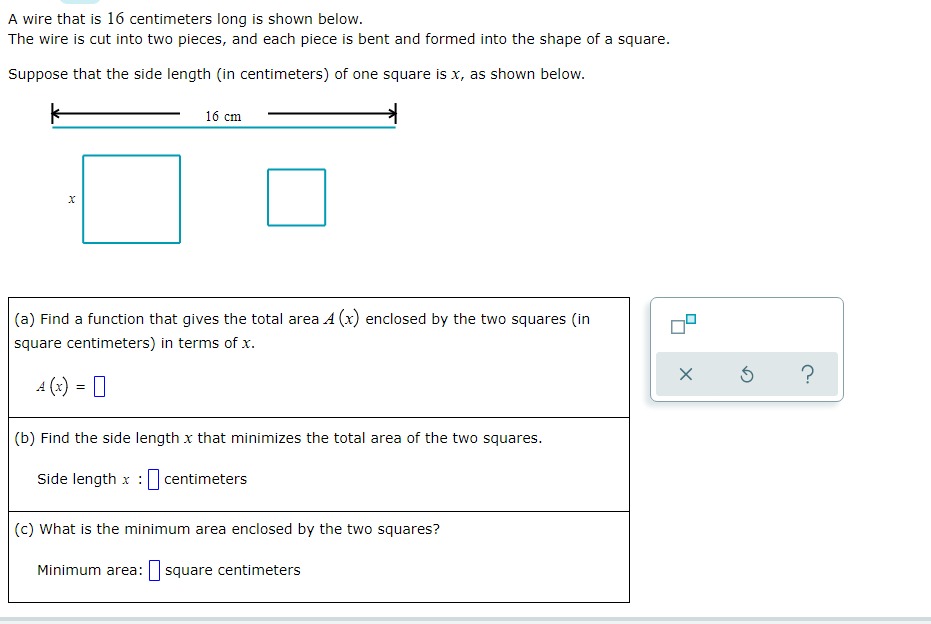
Question: A wire that is 16 centimeters long is shown below. The wire is cut into two pieces, and each piece is bent and formed into

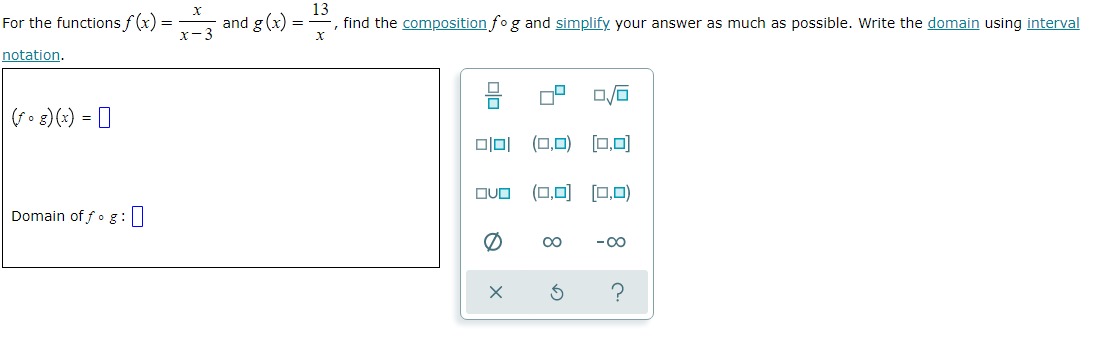
![X notation. ( f . 8) (x) = 1 Olol (0,0) [0,0]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667d877056e9a_704667d8770399fc.jpg)
![OVO (0,0] [0,0) Domain of fog : OO - OO X 5](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667d8770adbb9_704667d87708e678.jpg)
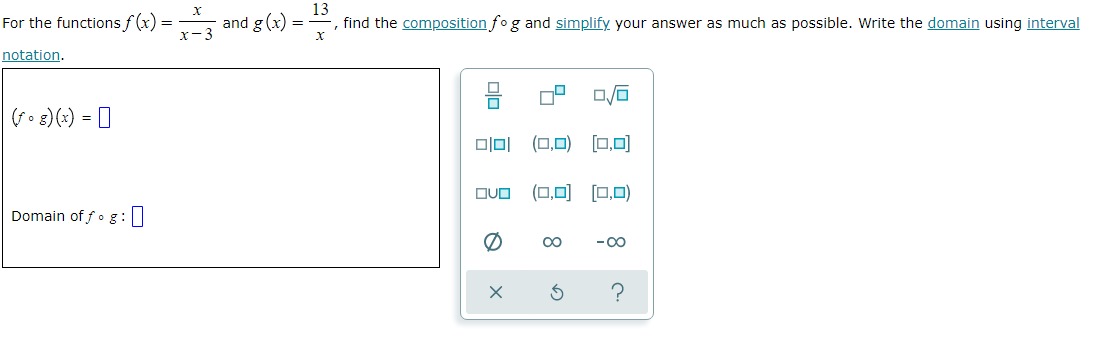
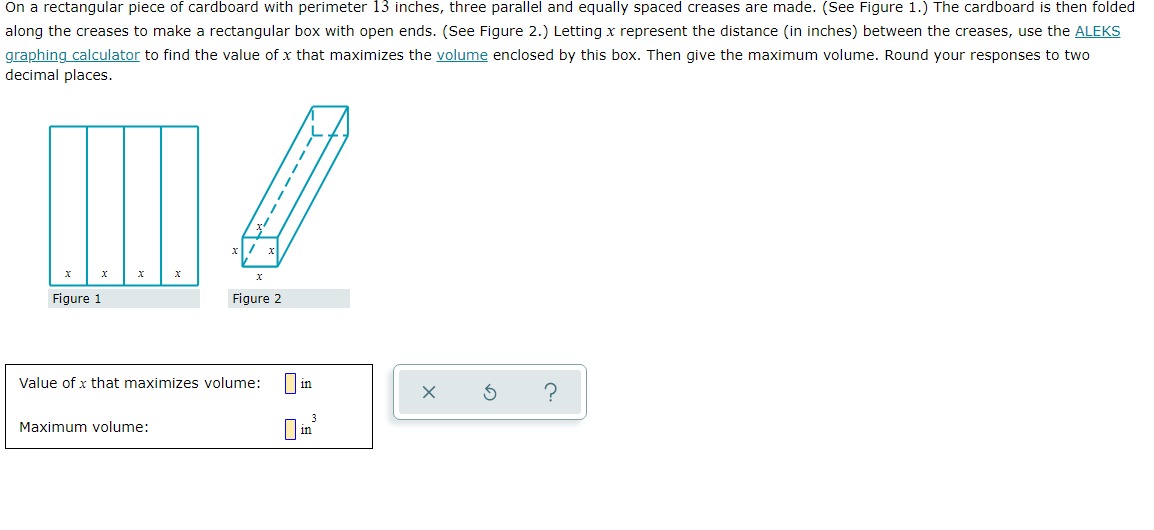
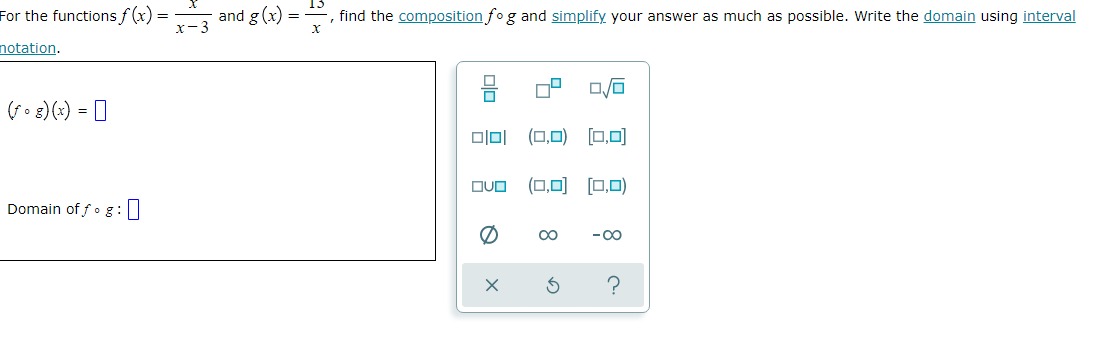
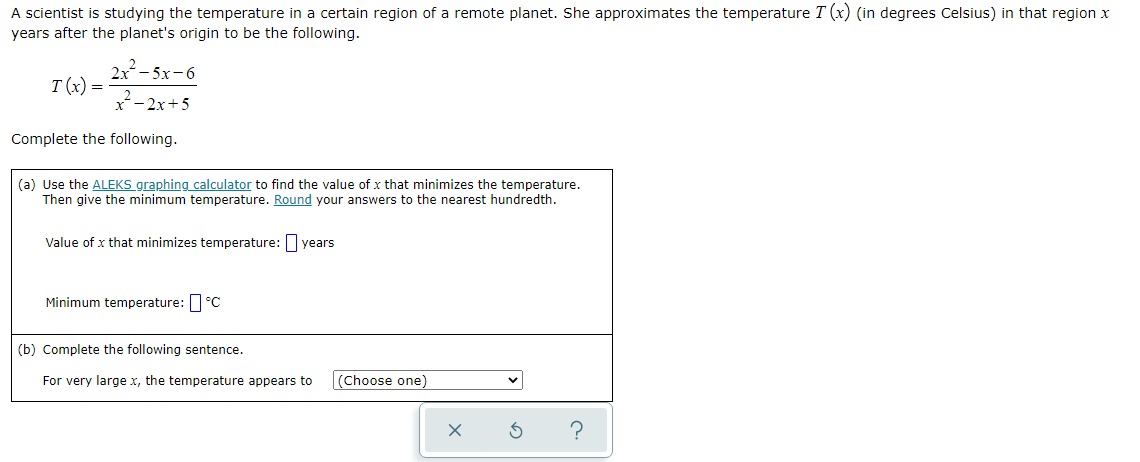
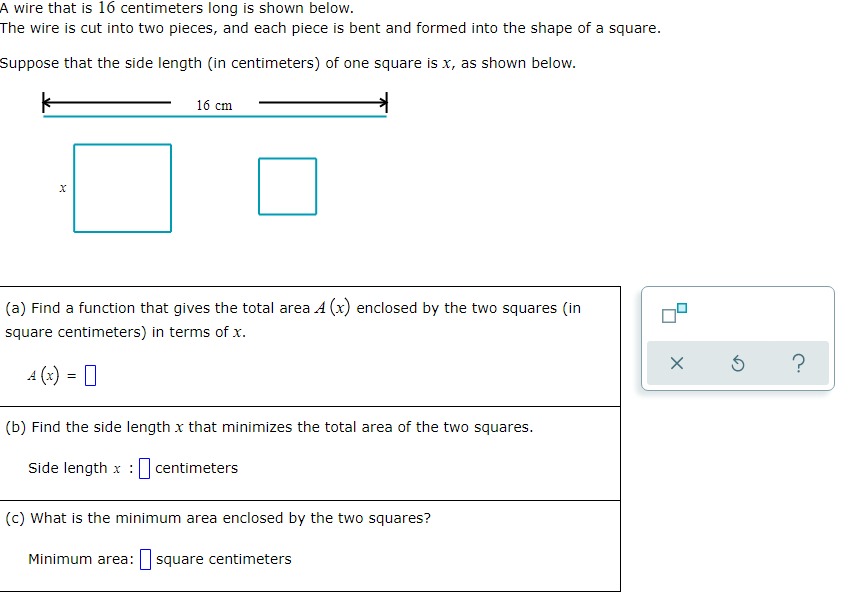
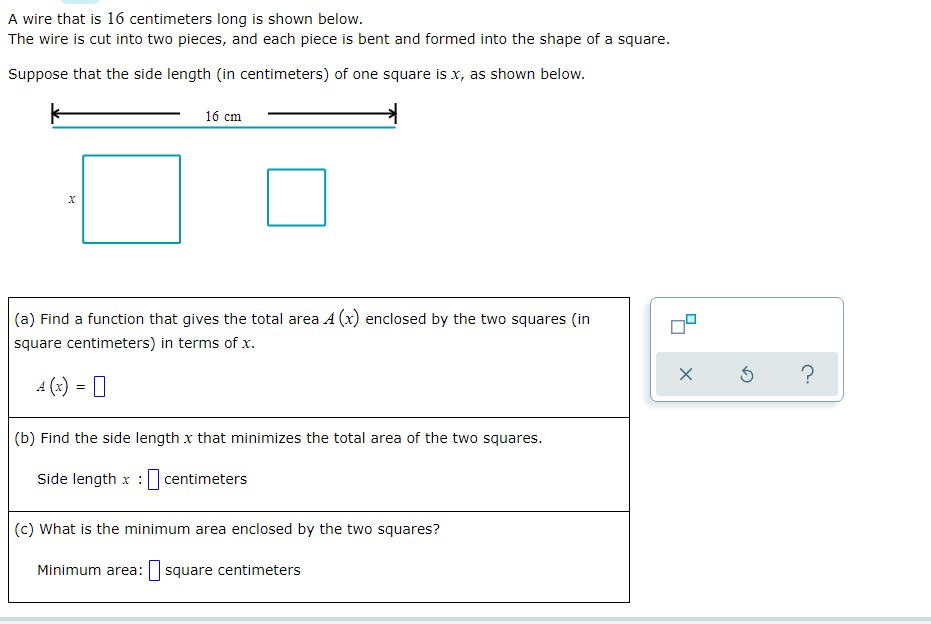
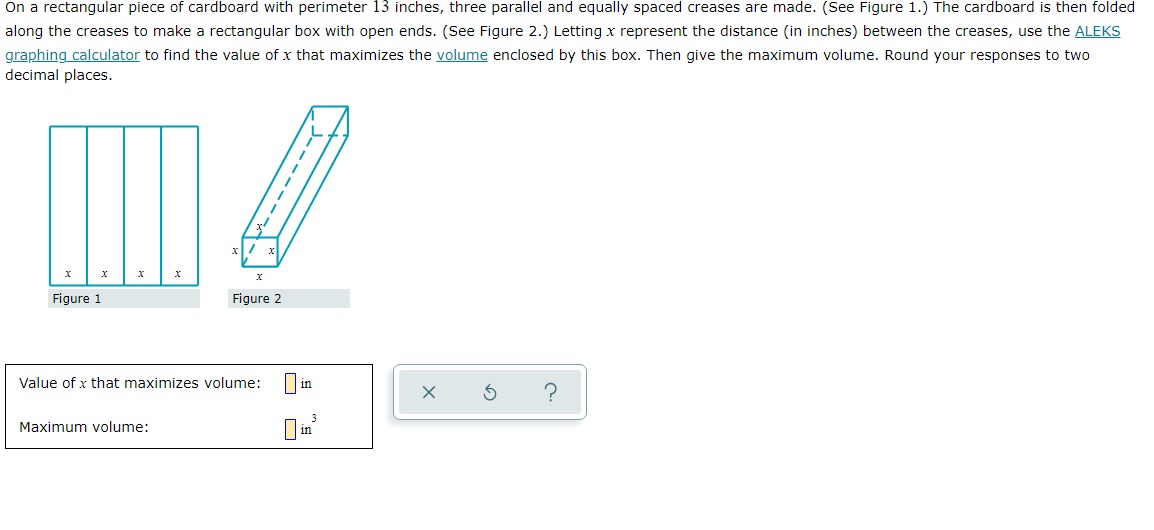
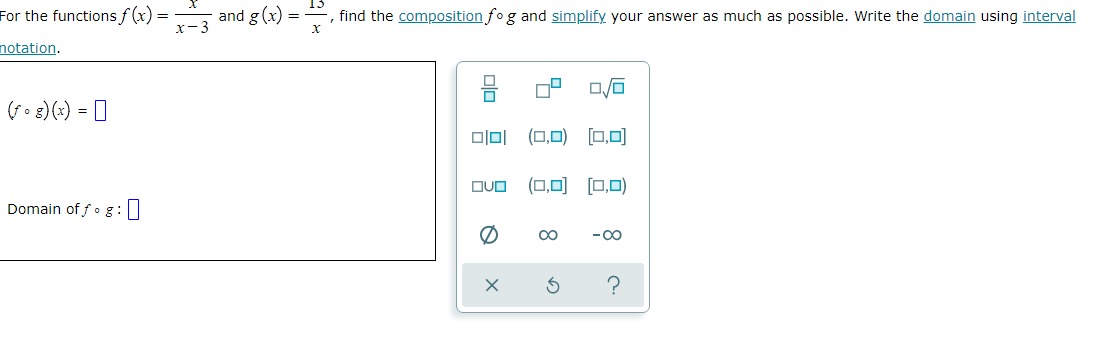
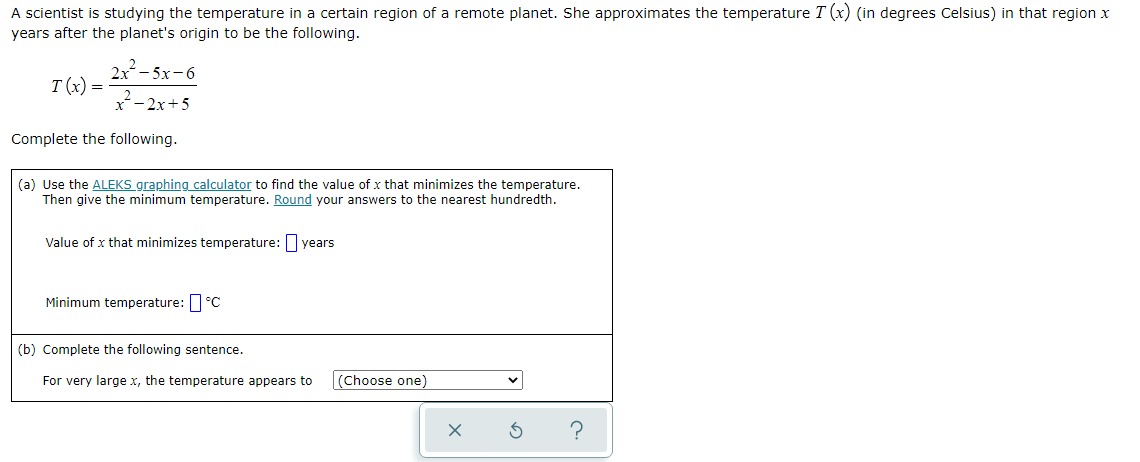
A wire that is 16 centimeters long is shown below. The wire is cut into two pieces, and each piece is bent and formed into the shape of a square. Suppose that the side length (in centimeters) of one square is x, as shown below. 16 cm X (a) Find a function that gives the total area A (x) enclosed by the two squares (in square centimeters) in terms of x. X A (x) = ? (b) Find the side length x that minimizes the total area of the two squares. Side length x : centimeters (c) What is the minimum area enclosed by the two squares? Minimum area: square centimetersX 13 For the functions f (x) = x - 3 and g (x) : , find the composition fog and simplify your answer as much as possible. Write the domain using interval X notation. ( f . 8) (x) = 1 Olol (0,0) [0,0] OVO (0,0] [0,0) Domain of fog : OO - OO X 5 ?On a rectangular piece of cardboard with perimeter 13 inches, three parallel and equally spaced creases are made. (See Figure 1. ) The cardboard is then folded along the creases to make a rectangular box with open ends. (See Figure 2.) Letting x represent the distance (in inches) between the creases, use the ALEKS graphing calculator to find the value of x that maximizes the volume enclosed by this box. Then give the maximum volume. Round your responses to two decimal places. X X X X Figure 1 Figure 2 Value of x that maximizes volume: in X 5 ? Maximum volume: in"For the functions f (x) = x - and g (xx) = - -, find the composition fog and simplify your answer as much as possible. Write the domain using interval notation. ( f . =) (x ) = 1 Olol (0,0) [0,0] OVO (0,0] [0,0) Domain of fog : OO - OO X 5 ?A scientist is studying the temperature in a certain region of a remote planet. She approximates the temperature 7 (x) (in degrees Celsius) in that region x years after the planet's origin to be the following. 2x- - 5x -6 T ( x) = x- - 2x +5 Complete the following. (a) Use the ALEKS graphing calculator to find the value of x that minimizes the temperature. Then give the minimum temperature. Round your answers to the nearest hundredth. Value of x that minimizes temperature: | years Minimum temperature: | -C (b) Complete the following sentence. For very large x, the temperature appears to (Choose one) v X ?For each pair of functions f and g below, find f(g (x)) and g (f(x)). Then, determine whether fand g are inverses of each other. Simplify your answers as much as possible. (Assume that your expressions are defined for all x in the domain of the composition. You do not have to indicate the domain.) (a) f (x) = x+6 (b ) f (xx ) X#0 4x g (x) = x - 6 X g (x) = 5 ? 4x fle (x) ) = 0 fle (x)) = 0 g(f(x)) = 0 8(f (x)) = 0 Of and g are inverses of each other Of and g are inverses of each other Of and g are not inverses of each other Of and g are not inverses of each otherA wire that is 16 centimeters long is shown below. The wire is cut into two pieces, and each piece is bent and formed into the shape of a square. Suppose that the side length (in centimeters) of one square is x, as shown below. ItlscmII (a) Find a function that gives the total areaA {x} enclosed by the two squares (in square centimeters) in terms of x. Am=o (b) Find the side length x that minimizes the total area of the two squares. Side length x : centimeters {c} What is the minimum area enclosed by the two squares? Minimum area: [I square centimeters
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


