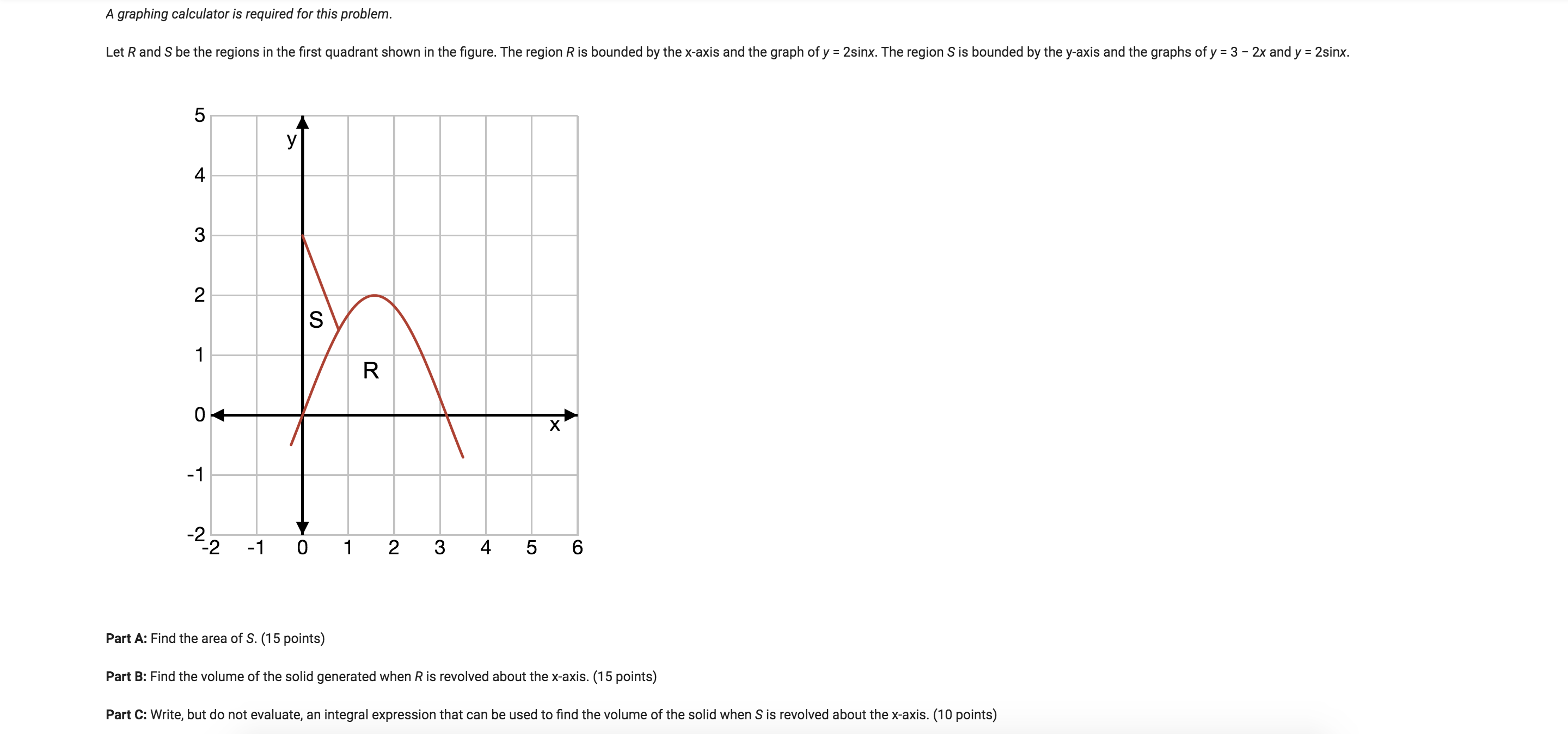
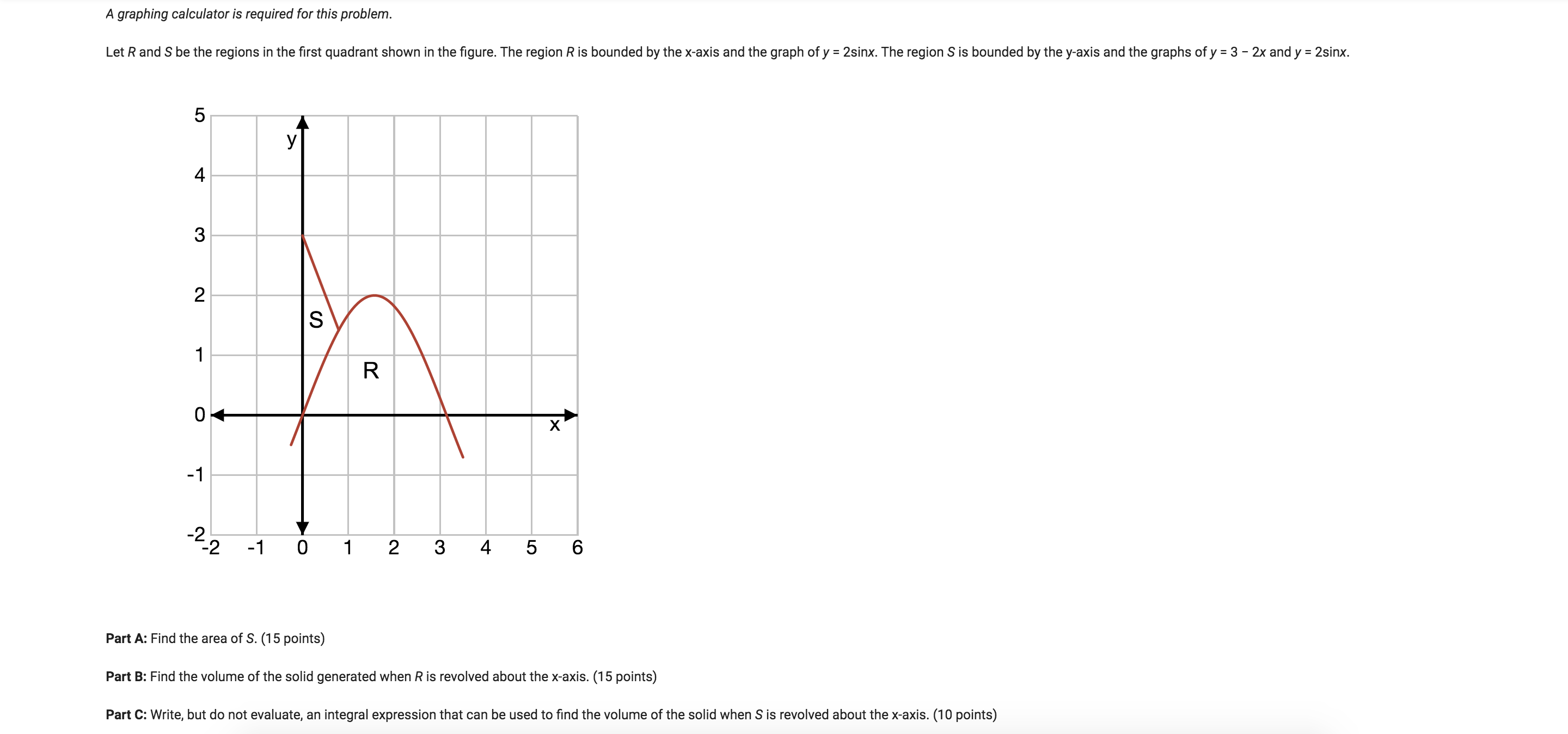
A yoyo is moving up and down a string so that its velocity at time t is given by v(t) = 4cos(t) for time t 2 0. The initial position of the yoyo at time t = 0 is x = 0,5], 2 (10 points) Part A: Find the average value of v(t) on the interval [ Part B: What is the displacement of the yo-yo from time t = 0 to time t = n? (10 points) Part C: Find the total distance the yoyo travels from time t = 0 to time t = 11. (10 points) y x2 - 7. For the regions bounded by y = 6cosx and 4 Part A: Find the limits of integration. (10 points) Part B: Write the expression representing the total area. (10 points) Part C: Solve for the total area. (10 points)A graphing calculator is required for this problem. Let R and S be the regions in the first quadrant shown in the figure. The region R is bounded by the x-axis and the graph of y = 2sinx. The region S is bounded by the y-axis and the graphs of y = 3 - 2x and y = 2sinx. 5 4 3 2 S R X -1 -2 2 -1 0 1 2 3 4 5 6 Part A: Find the area of S. (15 points) Part B: Find the volume of the solid generated when R is revolved about the x-axis. (15 points) Part C: Write, but do not evaluate, an integral expression that can be used to find the volume of the solid when S is revolved about the x-axis. (10 points)