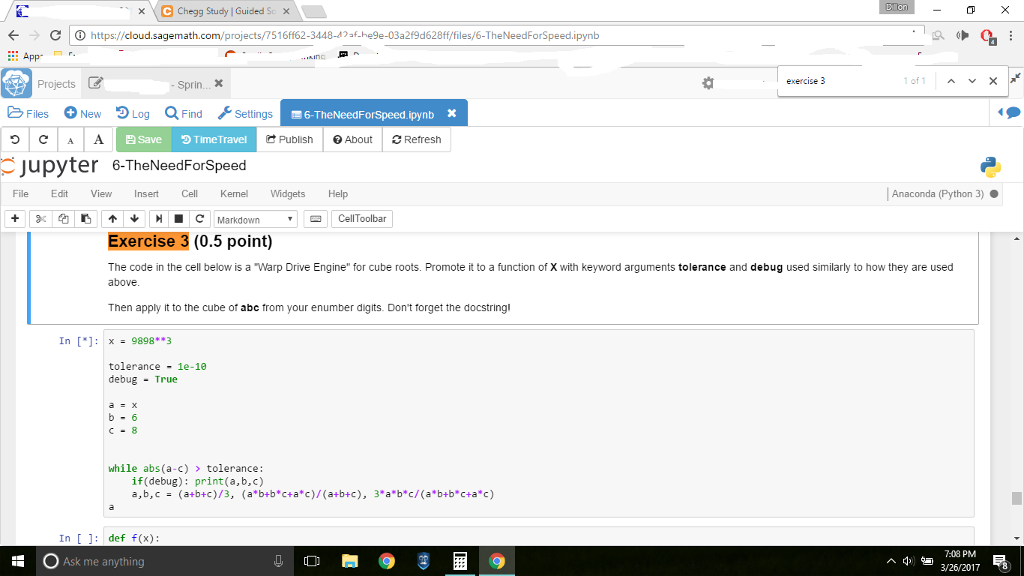
a=4

b=6

c=8

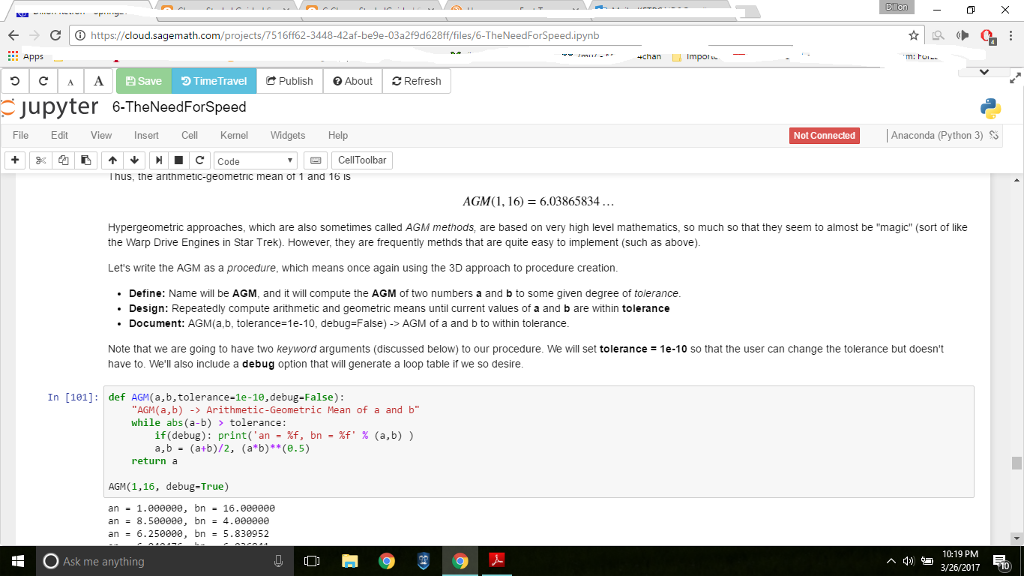
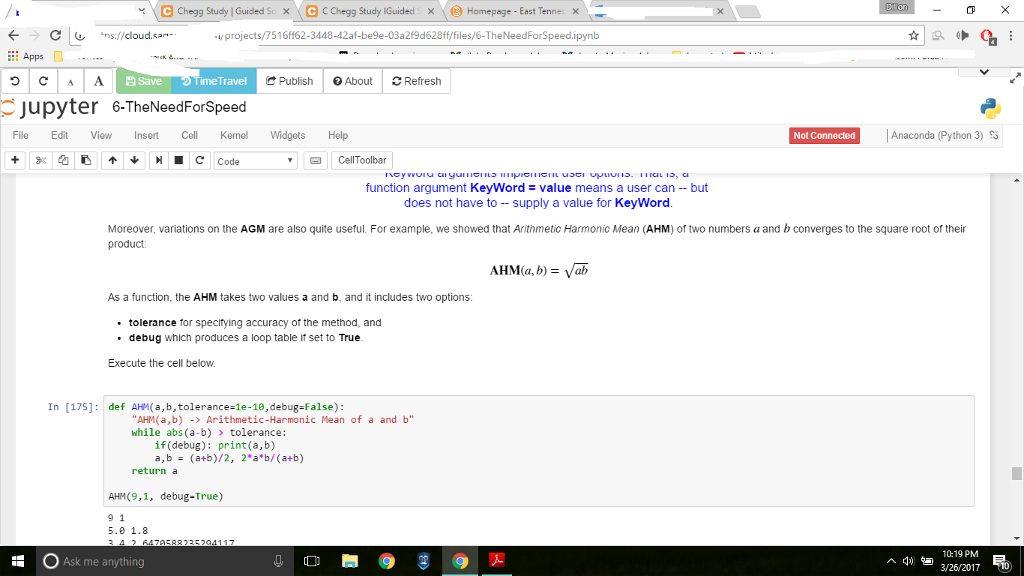
C O https://cloud sage ipynb math.com/proje CAA Save Time Travel Publish About CRefresh Jul pyter 6-TheNeedForspeed File Edit View Insert Cell Kernel Widgets Help Not Connected Anaconda (Python 3) SS inus, the arithmetic-geometric mean ot 1 and 16 IS AGM (1,160 6.03865834 Hypergeometric approaches, which are also sometimes called AGMi methods, are based on very high level mathematics, so much so that they seem to almost be "magic" sort of like the Warp Drive Engines in Star Trek). However, they are frequently methds that are quite easy to implement (such as above Let's write the AGM as a procedure. Which means once again using the 3D approach to procedure creation. Define Name will be AGM, and it will compute the AGM of two numbers a and b to some given degree of tolerance. Design: Repeatedly compute arithmetic and geometric means until current values of a and b are within tolerance Document AGM(a,b, tolerance 0, debug False) AGM of a and b to within tolerance Note that we are going to have two keyword arguments (discussed below) to our procedure. We will set tolerance 1e-10 so that the user can change the tolerance but doesn't have to. We'll also include a debug option that will generate a loop table if we so desire In 101 def AGM False (a,b,tolerance-1e-10, AGM(a,b) Arithmetic-Geometric Mean of a and b while abs (a-b) tolerance if(debug print ('an %f, bn 20f (a, b) a, b (a +b)/2, (a b)** Ge.5) return a AGM(1,16, debug-True) an 1.000000, bn 16.000000 an 8.500000 bn 4.000000 an 6.250000, bn 5.830952. 19 PM Ask me anything 3/26/2017 R100