• a.A small Engineering Consultancy seeks bids for an IT Helpdesk Provider to resolve day-to-day IT issues, and receives two offers, as follows:
  • Bytes for All an initial fee of 1000, and then 50 each week for troubleshooting services.
  • PC Wizards a weekly cost of 75 for troubleshooting services.

  Using a break-even chart, determine which of the two options is more economical, and after which point it becomes so. (In other words, which option will be of lower cost in the longer term. Consider a period of twelve months in your deliberations, and determine whether a point is reached where one option becomes cheaper than the other.)

  (10 marks)

• b.A window frame is shown in Figure 1 below. The thickness of the frame and the struts within the frame are small compared to the other dimensions, and do not need to be accounted for separately.

Figure 1 A window frame made up of four rectangles

Long description

• i.If 10 metres of frame are used to go around the outside perimeter of the window, show that w = (10 3h) / 4

  Explain each step of your working.

  (4 marks)

• ii.Show that the area of the window, A, can be expressed in terms of h by the quadratic equation: A = 7.5h 2.25h²

  Explain each step of your working.

  (4 marks)

• iii.Using the method described in Section 11.3 of the Part 3 book, find the overall dimensions of the frame (the height and width of the window) that make the area of the window a maximum.

  Explain each step of your working.

  (4 marks)

• iv.Using a spreadsheet, plot a graph showing the area of the window, A, as a function of h. Paste a copy of the graph into your TMA.

  (6 marks)

• v.Using the height and width of the window you found in part (iii) above, calculate the maximum area of the window. Compare this with the value shown in the graph you produced for part (iv) of this question.

  (2 marks)

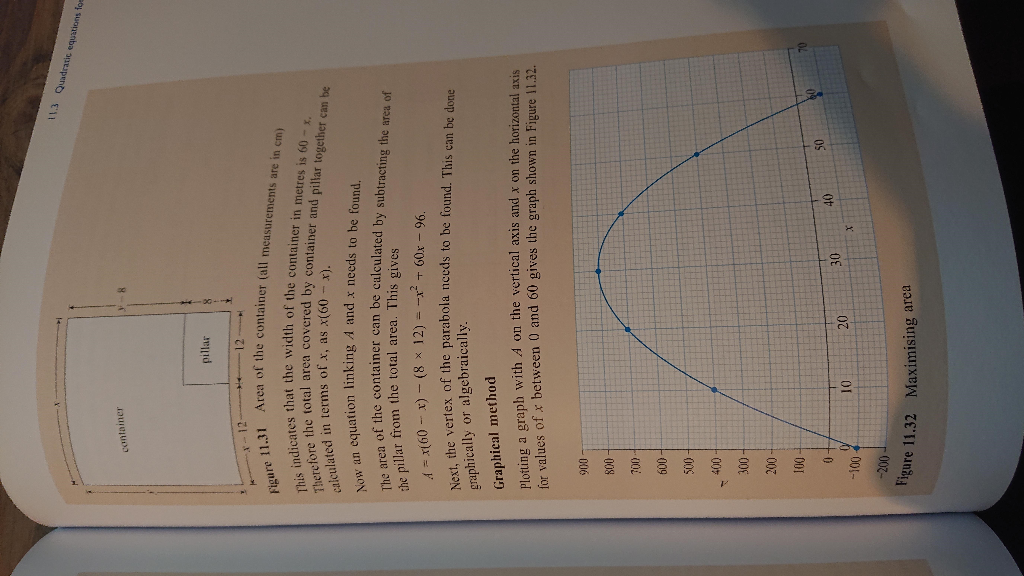
Example 11.8 Finding the area area of an enclosure se container to fit around design a multi-purpose container to might be used as a planter, base for a seal. The pillar has din u tainer will be made by bending h ibi CF, as a nibhish You You have been asked to design a multi-purpose rectangular pillar: the container mich bi bin for storage, or as the base for a seat. The Nem by 12 ani, and the container will be made metal 100 cm long into a four-sided shape comers of the pillar. Figure 11.30 illustra above. What is the maximum area that can be em arpillar: the storage, o he pillar has dimensions wade by bending a sheet shape that will buit up again ne 11.30 illustrates the situation at can be enclosed by the w ant two ation, viewed from container container pillar Area of the container (not drawn to scale) Figure 11.30 Solution First, choose the variables. The quantity to be maximised is the area of the container in m i will be represented by A. The variables that control the arca of the container are the length and width of the container in cm. These can be represented by x and y respectively, as shown in Figure 11.31. The first step is to write one of these in terms of the other (say, y in terms of x) so that an equation can be found relating the area, A, to just one of these variables. The perimeter of the container (the total length of the metal sheet) is 100ern, so (omitting units for clarity) (x - 12) + y + x + - 8) = 100. Simplifying this equation gives 2x + 2y - 20 = 100 and so x + y - 10 = 50. Making y the subject gives y = 60-x. 11.3 Quadratic equations for container pillar Figure 11.31 An the container (all measurements are in cm) This indicates that the Therefore the to calculated in term Now an equation linkin The area of the con e that the width of the container in metres is 60 - ered by container and pillar together can be lated in terms of x, as x(60 - x). equation linking A and x needs to be found. pillar from the total area. This gives the container can be calculated by subtracting the area of A x(60 - x) - (8 x 12) = -x + 60x - 96 the vertex of the parabola needs to be found. This can be done graphically or algebraically. Next, the vertex of the Dar Graphical method mating a graph with A on the vertical axis and x on the horizontal axis for values of x between 0 and 60 gives the graph shown in Figure 11.32. 900- 800 30 -1004 -2004 Figure 11.32 Maximising area Example 11.8 Finding the area area of an enclosure se container to fit around design a multi-purpose container to might be used as a planter, base for a seal. The pillar has din u tainer will be made by bending h ibi CF, as a nibhish You You have been asked to design a multi-purpose rectangular pillar: the container mich bi bin for storage, or as the base for a seat. The Nem by 12 ani, and the container will be made metal 100 cm long into a four-sided shape comers of the pillar. Figure 11.30 illustra above. What is the maximum area that can be em arpillar: the storage, o he pillar has dimensions wade by bending a sheet shape that will buit up again ne 11.30 illustrates the situation at can be enclosed by the w ant two ation, viewed from container container pillar Area of the container (not drawn to scale) Figure 11.30 Solution First, choose the variables. The quantity to be maximised is the area of the container in m i will be represented by A. The variables that control the arca of the container are the length and width of the container in cm. These can be represented by x and y respectively, as shown in Figure 11.31. The first step is to write one of these in terms of the other (say, y in terms of x) so that an equation can be found relating the area, A, to just one of these variables. The perimeter of the container (the total length of the metal sheet) is 100ern, so (omitting units for clarity) (x - 12) + y + x + - 8) = 100. Simplifying this equation gives 2x + 2y - 20 = 100 and so x + y - 10 = 50. Making y the subject gives y = 60-x. 11.3 Quadratic equations for container pillar Figure 11.31 An the container (all measurements are in cm) This indicates that the Therefore the to calculated in term Now an equation linkin The area of the con e that the width of the container in metres is 60 - ered by container and pillar together can be lated in terms of x, as x(60 - x). equation linking A and x needs to be found. pillar from the total area. This gives the container can be calculated by subtracting the area of A x(60 - x) - (8 x 12) = -x + 60x - 96 the vertex of the parabola needs to be found. This can be done graphically or algebraically. Next, the vertex of the Dar Graphical method mating a graph with A on the vertical axis and x on the horizontal axis for values of x between 0 and 60 gives the graph shown in Figure 11.32. 900- 800 30 -1004 -2004 Figure 11.32 Maximising area