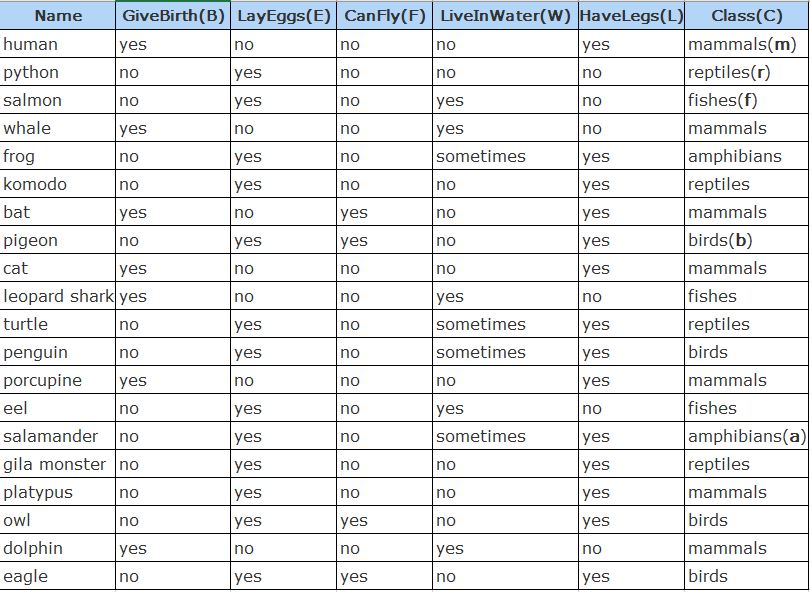
Question: a)As we are going to classify , we need to calculate conditional probabilities for P(B=0|C=m), P(E=1|C=m), P(F=0|C=m), P(W=0.5|C=m), P(L=1|C=m).The same calculation needs to be done
a)As we are going to classify , we need to calculate conditional probabilities for P(B=0|C=m), P(E=1|C=m), P(F=0|C=m), P(W=0.5|C=m), P(L=1|C=m).The same calculation needs to be done for C=b, C=a, C=r, and C=f.
If you cannot remember the formula for conditional probabilities, the following will help:
Let N(B=0, C=m) be the number of tuples having B=0 and C=m.
P(B=0|C=m) is N(B=0, C=m) / N(C=m)
P(B=0,E=1|C=m)= N(B=0, E=1, C=m) / N(C=m)
P(B=0|C=m,E=1)= N(B=0, E=1, C=m) / N(C=m,E=1)
b)Use the naive Bayes approach and the conditional probabilities calculated in (a) to predict the class label for the test tuple . Note that nave Bayesian assumes the independence among the input variables B,E,F,W, and L, thus
P(B=0,E=1,F=0,W=0.5,L=1|C=m)
= P(B=0|C=m)*P(E=1|C=m)*P(F=0|C=m)*P(W=0.5|C=m)*P(L=1|C=m)
The probability of the tuple having class m is
P(C=m | B=0,E=1,F=0,W=0.5,L=1)
= P(B=0,E=1,F=0,W=0.5,L=1|C=m)* P(C=m) / P(B=0,E=1,F=0,W=0.5,L=1)
c)Remove the correlated column E and use the nave Bayesian to do the classification again for the test tuple .
d)Compare b) and c) and explain whether the removal of E helps make the classification better or worse.
\f
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


