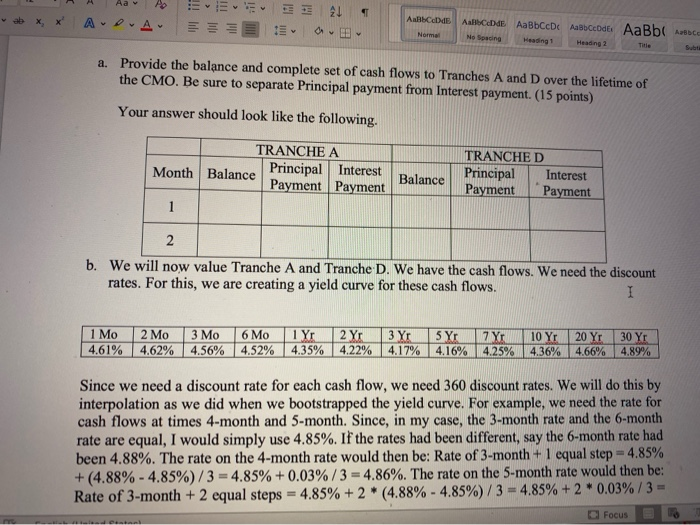
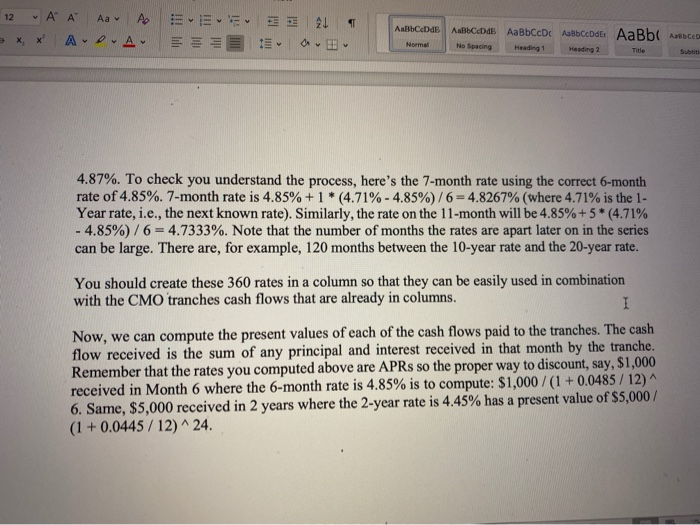
Aav 21 1 Au AlbceDdE Normal Aalib ceDdE AaBbCcDc Accode AaBb Ace Heading Heading 2 Subt. No Spacing Title a. Provide the balance and complete set of cash flows to Tranches A and D over the lifetime of the CMO. Be sure to separate Principal payment from Interest payment. (15 points) Your answer should look like the following. TRANCHE A Month Balance Principal Interest Payment Payment Balance TRANCHED Principal Interest Payment Payment 2 b. We will now value Tranche A and Tranche D. We have the cash flows. We need the discount rates. For this, we are creating a yield curve for these cash flows. I 1 Mo 2 Mo 3 Mo 6 Mo 1 Yr 2 Yr 3 Yr 4.61% 4.62% 4.56% 4.52% 4.35% 4.22% 4.17% 5 Yr 4.16% 7 Yr 4.25% 10 Yr 4.36% 20 Yr 4.66% 30 Yr 4.89% Since we need a discount rate for each cash flow, we need 360 discount rates. We will do this by interpolation as we did when we bootstrapped the yield curve. For example, we need the rate for cash flows at times 4-month and 5-month. Since, in my case, the 3-month rate and the 6-month rate are equal, I would simply use 4.85%. If the rates had been different, say the 6-month rate had been 4.88%. The rate on the 4-month rate would then be: Rate of 3-month + 1 equal step=4.85% +(4.88% -4.85%)/3 = 4.85% +0.03%/3 = 4.86%. The rate on the 5-month rate would then be: Rate of 3-month + 2 equal steps 4.85% + 2 * (4.88% - 4.85%)/3 = 4.85% + 2 * 0.03%/3 Focus Det 12 ' T A EEEE 21 D-A E E ABCD AaBbCcDc ABCcDdEt AaBb Asbe A Normal No Spacing Heading 1 Heading 2 Title Subtit 4.87%. To check you understand the process, here's the 7-month rate using the correct 6-month rate of 4.85%. 7-month rate is 4.85% +1* (4.71% - 4.85%)/6 =4.8267% (where 4.71% is the 1- Year rate, i.e., the next known rate). Similarly, the rate on the 11-month will be 4.85%+5 * (4.71% - 4.85%)/6 = 4.7333%. Note that the number of months the rates are apart later on in the series can be large. There are, for example, 120 months between the 10-year rate and the 20-year rate. You should create these 360 rates in a column so that they can be easily used in combination with the CMO tranches cash flows that are already in columns. I Now, we can compute the present values of each of the cash flows paid to the tranches. The cash flow received is the sum of any principal and interest received in that month by the tranche. Remember that the rates you computed above are APRs so the proper way to discount, say, $1,000 received in Month 6 where the 6-month rate is 4.85% is to compute: $1,000 / (1 + 0.0485/12) 6. Same, $5,000 received in 2 years where the 2-year rate is 4.45% has a present value of $5,000/ (1 + 0.0445/12)^24. Aav 21 1 Au AlbceDdE Normal Aalib ceDdE AaBbCcDc Accode AaBb Ace Heading Heading 2 Subt. No Spacing Title a. Provide the balance and complete set of cash flows to Tranches A and D over the lifetime of the CMO. Be sure to separate Principal payment from Interest payment. (15 points) Your answer should look like the following. TRANCHE A Month Balance Principal Interest Payment Payment Balance TRANCHED Principal Interest Payment Payment 2 b. We will now value Tranche A and Tranche D. We have the cash flows. We need the discount rates. For this, we are creating a yield curve for these cash flows. I 1 Mo 2 Mo 3 Mo 6 Mo 1 Yr 2 Yr 3 Yr 4.61% 4.62% 4.56% 4.52% 4.35% 4.22% 4.17% 5 Yr 4.16% 7 Yr 4.25% 10 Yr 4.36% 20 Yr 4.66% 30 Yr 4.89% Since we need a discount rate for each cash flow, we need 360 discount rates. We will do this by interpolation as we did when we bootstrapped the yield curve. For example, we need the rate for cash flows at times 4-month and 5-month. Since, in my case, the 3-month rate and the 6-month rate are equal, I would simply use 4.85%. If the rates had been different, say the 6-month rate had been 4.88%. The rate on the 4-month rate would then be: Rate of 3-month + 1 equal step=4.85% +(4.88% -4.85%)/3 = 4.85% +0.03%/3 = 4.86%. The rate on the 5-month rate would then be: Rate of 3-month + 2 equal steps 4.85% + 2 * (4.88% - 4.85%)/3 = 4.85% + 2 * 0.03%/3 Focus Det 12 ' T A EEEE 21 D-A E E ABCD AaBbCcDc ABCcDdEt AaBb Asbe A Normal No Spacing Heading 1 Heading 2 Title Subtit 4.87%. To check you understand the process, here's the 7-month rate using the correct 6-month rate of 4.85%. 7-month rate is 4.85% +1* (4.71% - 4.85%)/6 =4.8267% (where 4.71% is the 1- Year rate, i.e., the next known rate). Similarly, the rate on the 11-month will be 4.85%+5 * (4.71% - 4.85%)/6 = 4.7333%. Note that the number of months the rates are apart later on in the series can be large. There are, for example, 120 months between the 10-year rate and the 20-year rate. You should create these 360 rates in a column so that they can be easily used in combination with the CMO tranches cash flows that are already in columns. I Now, we can compute the present values of each of the cash flows paid to the tranches. The cash flow received is the sum of any principal and interest received in that month by the tranche. Remember that the rates you computed above are APRs so the proper way to discount, say, $1,000 received in Month 6 where the 6-month rate is 4.85% is to compute: $1,000 / (1 + 0.0485/12) 6. Same, $5,000 received in 2 years where the 2-year rate is 4.45% has a present value of $5,000/ (1 + 0.0445/12)^24