about random distribution, normal distribution

AND probability

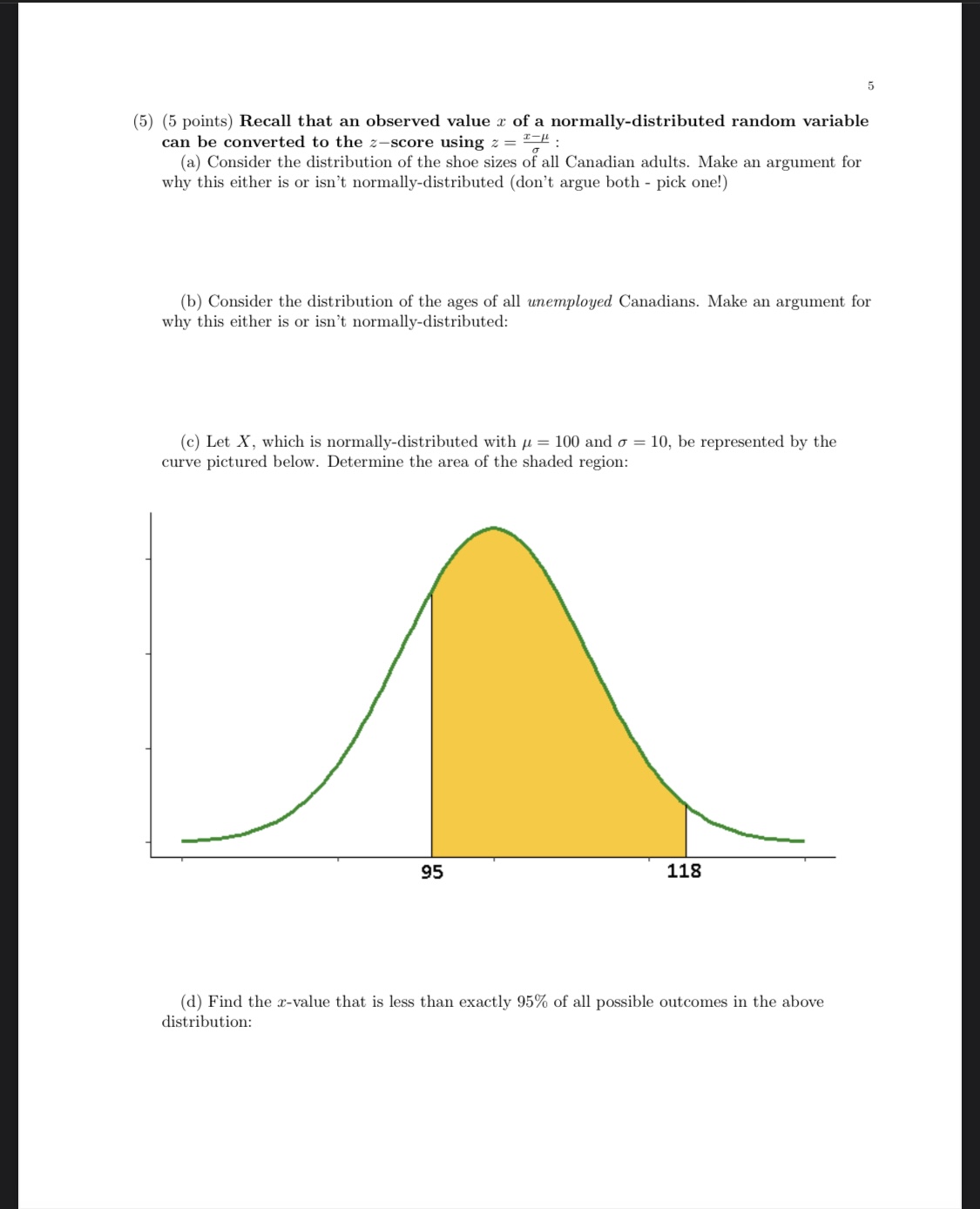
5 (5) (5 points) Recall that an observed value :2: of a normally-distributed random variable can be converted to the zscore using 2 = 125 : (a) Consider the distribution of the shoe sizes of all Canadian adults. Make an argument for why this either is or isn't normally-distributed (don't argue both - pick one!) (b) Consider the distribution of the ages of all unemployed Canadians. Make an argument for why this either is or isn't normally-distributed: (e) Let X , which is normally-distributed with u = 100 and cr = 10, be represented by the curve pictured below. Determine the area of the shaded region: 95 118 ((1) Find the x-value that is less than exactly 95% of all possible outcomes in the above distribution: (3) (5 points) A recent news article noted that most people who win the US presidential election tend to do so on their rst try - in fact, in the past century, this is true in 75% of cases. However, the opposite is not true: most people who run for president for the rst time do not win. For a randomly-selected candidate for president in the past century, let W represent the event \"they won the election\(4) (5 points} Consider the events A,B, and C in a sample space S, and suppose we know nothing about the events except the following: P(A} = 0.5, P(0.5} = B, P(C) = 0.3, P(A n C) = 0.75, P(A U C) = 0.25, P(AU B U C) = 1.3, and PK?!) = 0.3. (a) Identify at least four mistakes above: (b) Suppose a statistics exam has 8 problems on it, each covering just. one of 10 total topics with none being repeated. How many different possible exams can there be? Does this describe a permutation or a combination? Argue your choice in detail: (c) How may different ways can you reorder the digits in your student ID? (d) On a very slow day, a restaurant averages 4 customers in the hours from 2:00-3:00, though sometimes fewer customers arrive, and sometimes more. Let X be the number of customers showing up in that one hour space of time and answer the following: (i) Find E(X) and V(X}, (ii) Determine whether X is discrete or continuous (as always, explain why), (iii) Find the probability of no customers showing up, and (iv) Find the probability of at least one customer showing up