ABOVE IS WHAT I NEED SOLVED - BELOW IS EXACTLY HOW TO SOLVE IT, I JUST NEED THE DATA FROM ABOVE INPUT INTO THEIR RESPECTIVE AREA BELOW AND SOLVED. THANK YOU SO VERY MUCH!!!

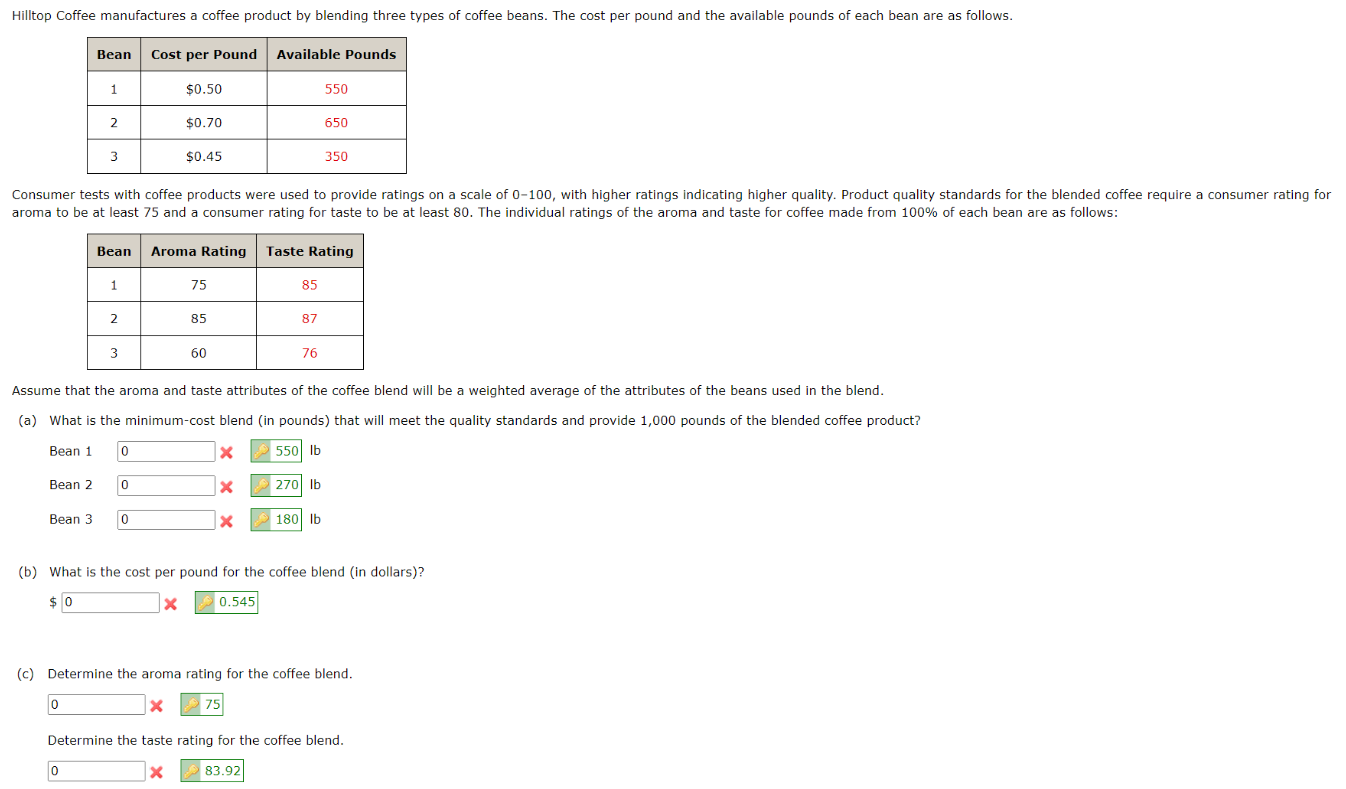
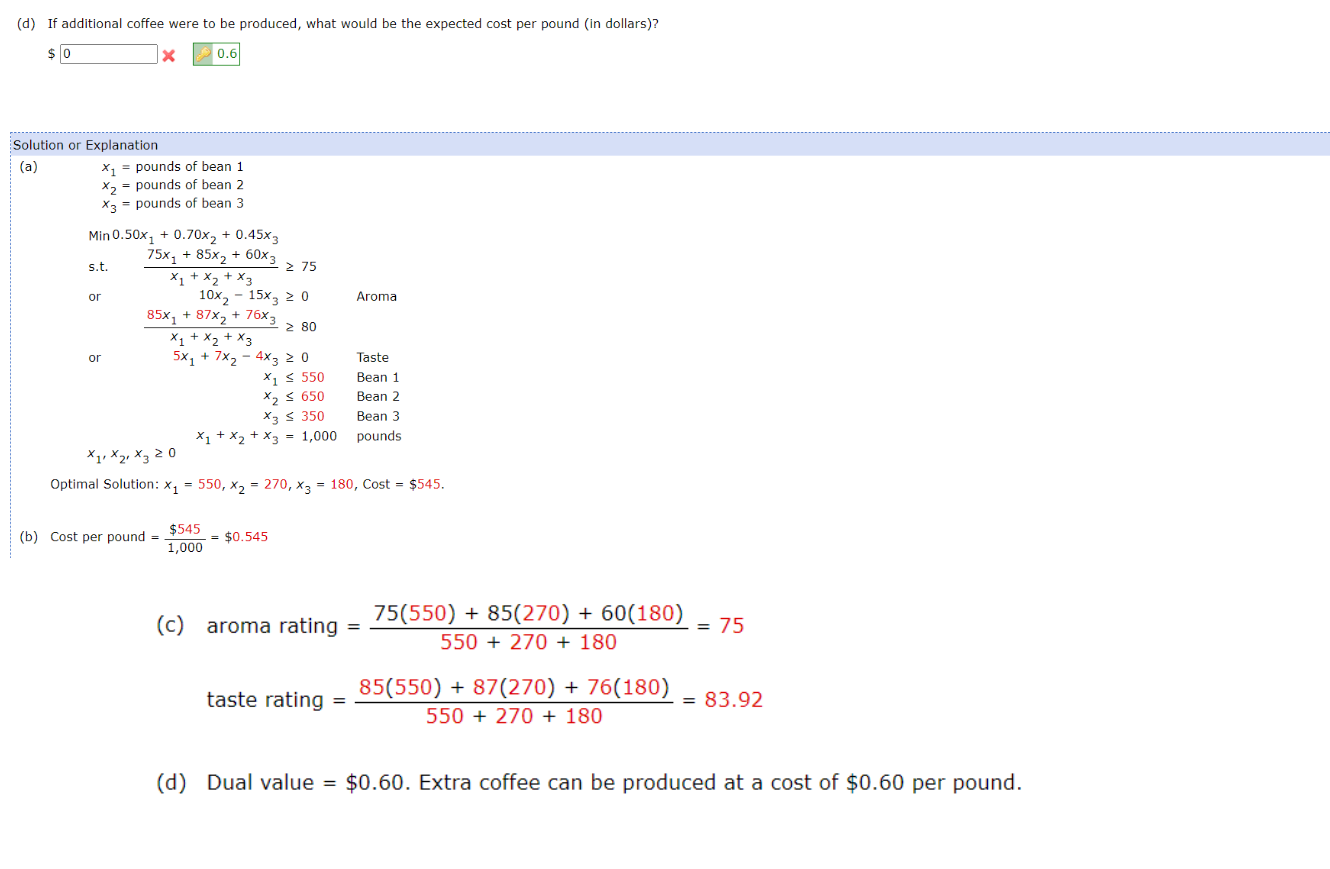
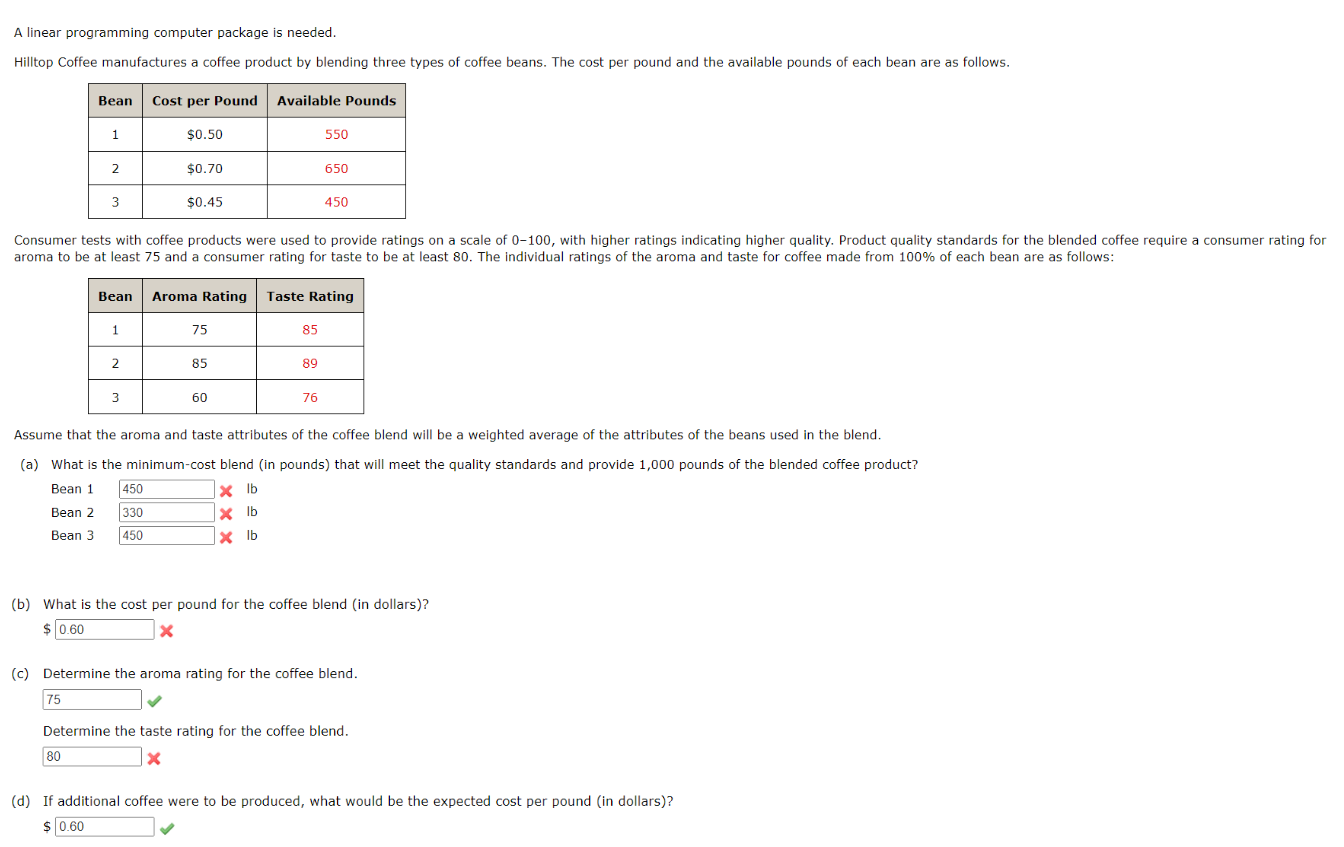
A linear programming computer package is needed. Hilltop Coffee manufactures a coffee product by blending three types of coffee beans. The cost per pound and the available pounds of each bean are as follows. aroma to be at least 75 and a consumer rating for taste to be at least 80 . The individual ratings of the aroma and taste for coffee made from 100% of each bean are as follows: Assume that the aroma and taste attributes of the coffee blend will be a weighted average of the attributes of the beans used in the blend. (a) What is the minimum-cost blend (in pounds) that will meet the quality standards and provide 1,000 pounds of the blended coffee product? Bean 1 Bean 2 Bean 3 lb lb lb (b) What is the cost per pound for the coffee blend (in dollars)? $ (c) Determine the aroma rating for the coffee blend. Determine the taste rating for the coffee blend. (d) If additional coffee were to be produced, what would be the expected cost per pound (in dollars)? (b) What is the cost per pound for the coffee blend (in dollars)? $ X (c) Determine the aroma rating for the coffee blend. Determine the taste rating for the coffee blend. (d) If additional coffee were to be produced, what would be the expected cost per pound (in dollars)? Solution or Explanation (a) x1=poundsofbean1x2=poundsofbean2x3=poundsofbean3Min0.50x1+0.70x2+0.45x3s.t.x1+x2+x375x1+85x2+60x375or10x215x30x1+x2+x385x1+87x2+76x3805x1+7x24x30x1550Bean1x2650Bean2x3350Bean3x1,x2,x30x1+x2+x3=1,000pounds Aroma or Taste Optimal Solution: x1=550,x2=270,x3=180, Cost =$545. (b) Cost per pound =1,000$545=$0.545 (c)aromarating=550+270+18075(550)+85(270)+60(180)=75tasterating=550+270+18085(550)+87(270)+76(180)=83.92 (d) Dual value =$0.60. Extra coffee can be produced at a cost of $0.60 per pound