Abstract Algebra

Solve #1(a)-(d). Give ALL steps and proof.

GIVE ORIGINAL ANSWER!

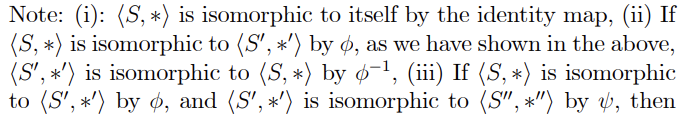
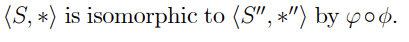
1. [pts] Let (S, *) and (S', *) be any given two binary structures. Let o : S - S' be any given isomorphism from (S, *) to (S", *'). Let us show that the inverse map o : S' - S exists, and is an isomorphism from (S', *) to ( S, *). (a) Define a map - from S' to S by o (s') = s if and only if o (s) = s'. Show that o- is well-defined as a map. (b) Show that o-1 : S' - S is one-to-one. (c) Show that o ] : S' - S is onto. (d) Show that o ]: S' - S preserves the operations.Note: (i): (S,*) is isomorphic to itself by the identity map: (ii) If (S, 1:) is isomorphic to (5', an') by a, as we have shown in the above, (3', *') is isomorphic to (S, 1:) by (ill13 (iii) If (S, 4:) is isomorphic to (3',*') by qb, and (52:45) is isomorphic to (S\(S, *) is isomorphic to * by yoo