Abstract Geometry! Please only answer if 100% confident. Will rate thumbs up if correct!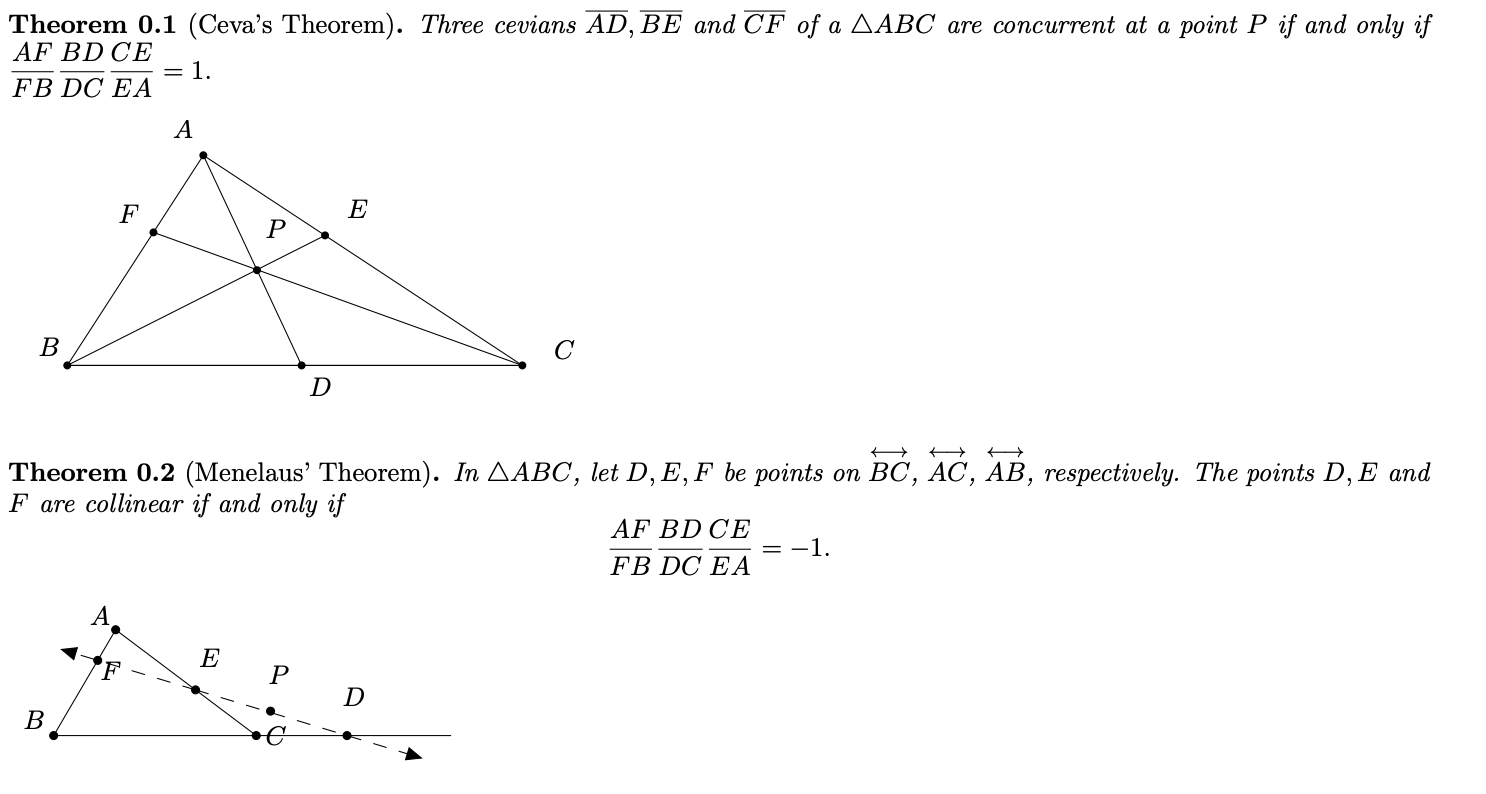

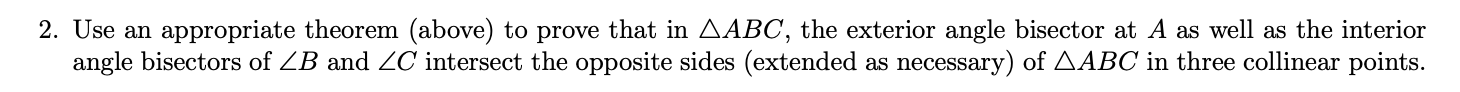
Theorem 0.1 (Cevas Theorem). Three cevians AD, BE and CF of a AABC are concurrent at a point P if and only if AF BDCE = 1. FB DC EA A F E B D Theorem 0.2 (Menelaus Theorem). In AABC, let D, E, F be points on BC, AC, AB, respectively. The points D, E and F are collinear if and only if AF BD CE FB DC EA -1. . E YF D B 2. Use an appropriate theorem (above) to prove that in AABC, the exterior angle bisector at A as well as the interior angle bisectors of ZB and ZC intersect the opposite sides (extended as necessary) of AABC in three collinear points