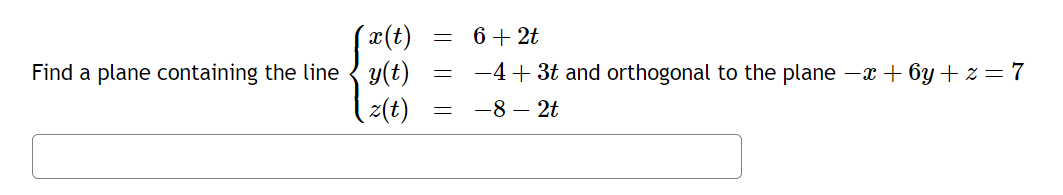
ac (t) = 8 + 3t Find a plane containing the point (4, 1,-2) and the line y(t) = 3- 2t z (t ) = 1+2tac (t) = 6+2t Find a plane containing the line y(t ) = -4 + 3t and orthogonal to the plane -xx + 6y + z = 7 z(t ) = -8 - 2t1. Given . Point ( U, ' , - 2 ) = B . classmate dine * ( ) ) = 8 +3+ Date Page y ( + ) = 3-21 2 ( f ) = 1+ 2 + . * A line Parallel to the vector y? = (a, bic) Passing through the point A ( ) 1 , y , , 2 , ) is given by the parametric Equations . y = y , + 67 (compain(" with above equations) 2 = 2+ ct 18 A = ( 8 , 3 , 1 ) ON L V = ( 3 1 - 2 2 ) leu y - AB = ( u , l, - 2 ) - ( 37 27 2 8, 3 , 1 ) ( vector along AB ) - (41 - 2 1 - 3) UN = ( 312 , 2 ) . 1 = xV ( normal vection ) = i ( - 4 1 - 21 - 3 ) x ( 3 1 - 2 , 2 ) K . -U - 2 -3 I i ( (2 X 2 ) - ( - 3X - 2 ) ) # 1 ( 1 - 4x2) - (3x 3 - 2 9 + k ( ( - ux - 2 ) - ( 3 x - 2 ) ) = 1 6-4-6) #j (-8+9) th (8+6) D z- 101 -7 + luk ( normal vector), (-10, - 1,14)". Equation of plane containing the point B ( 21 1 , 4 , 2 , ) = ( 4, 1 , - 2 ) and having anormal vector ? ( a, b, c ) = ( - 10, -1 , 14) is a ( x - x , ) + b ( y - y , ) + c ( 2 - 2 , ) - 0. -8 28 . = ) - 10 ( ) ( - 4 ) 4 - 1 ( 4 - 1 ) + 14 ( 7+2 ) = 0. - 10x + 40 - 4 + 1 + 142+28 = 0 - 10 x 1 - y + 142 - 69 = 0