Question: Exercise 6. Let (X, d) be a metric space. Given E C X, let E be the set of interior points of E. (The

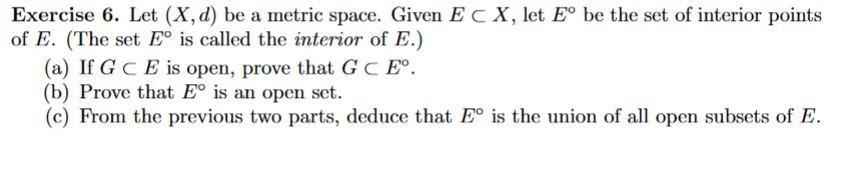
Exercise 6. Let (X, d) be a metric space. Given E C

Exercise 6. Let (X, d) be a metric space. Given E C X, let E be the set of interior points of E. (The set E is called the interior of E.) (a) If GCE is open, prove that G C E. (b) Prove that E is an open set. (c) From the previous two parts, deduce that E is the union of all open subsets of E.

Step by Step Solution

★★★★★

3.48 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

int E xcE x is an interion point of Ef Let point of E ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Physics Questions!

FINA 480 Case assignment #2 Clarkson Lumber Company This case is an investigation of short-term debt financing decisions. You are asked to write up a professional memo representing either Mr....

Grizzly Bear Winery (GBW) is a small winery in Portland, OR. Kerry Smith is the CEO and President of the Board of Directors, which is made-up of local business owners and professionals. In 2018, GBW...

Present value can be used to determine the fair price -or value - of a bond. In the examples that follow, assume you are working with zero-coupon bond and that there are no transaction costs. A...

A magnetic field can be used to determine the sign of charge carriers in a current- carrying wire. Consider a wide conducting strip in a magnetic field oriented as shown in Fig. 19.34. The charge...

The temperatures recorded during the summer and winter in a particular locality are 45 C and 15 C respectively: a. If air is used as a cooling medium having a temperature difference of 15 C,...

EXAM II: PRACTICE SHEET (1) All the HW problems! (2) (a) Let (X, d) be a metric space. Prove that the closed neighborhood N r (x) = {y X : d(x, y) r} is a closed set. (b) Let (Rn , d) with the...

Kindly solve the following questions. 8. Find a limit point for the set {-1 : ne ( ). Bolzano 9. Let A = {-1 : ne N}. a) Find A in R. b) Explain why A is a compact subset of H. 10. Let X be a compact...

Convex geometry 0.1 Dehn-Sommerville relations In this section we will talk about convex polytopes. One possible denition of a convex polytope uses the notion of a half-space: A closed half-space in...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

DIRECTIONS: For each of the following questions, you may only site propositions 6.1, 7.1, 7.2, and 7.3; the incidence axioms, the betweenness axioms, and any definition from sections 6 & 7 of...

Galileo devised a simple terrestrial telescope that produces an upright image. It consists of a converging objective lens and a diverging eyepiece at opposite ends of the telescope tube. For distant...

A continuous random variable X is said to have a uniform distribution on the interval [a, b] if the PDF has the form (a) Find the probability that the value of A' is closer to a than it is to b. (b)...

What comparison series would you use with the Limit Comparison Test lo determine whether k = 1 k 2 k 5 k 3 3 k 1 converges Choces, he conect answer below. A . k = 1 k B . k = 1 1 k c k = 1 1 k 2 p ....

Mountain Tea Co. makes two products: a high-grade tea branded Wulong and a low-grade tea branded San Tea for the Asian market. Mountain purchases tea leaves from tea firms in mountainous villages of...

Choose a product. Conduct a branded and unbranded experiment. What do you learn about the equity of the brands in that product class?

How does a positioning map work? What are its benefits?

What are the six categories generally used to position a product?

Create a professional marketing research brief for the CEO of an organization. Develop the brief as if it will be later incorporated into a complete marketing plan, including the following: Marketing...

Financial records help track school income and expenditure. Select one: True False

Consider again the conditions of Exercise 9. Let X denote a random variable for which the c.d.f. is F(x), and let Y denote a random variable for which the c.d.f. is G(x). Use the Kolmogorov-Smirnov...

For the problem described in Exercise 9, let X denote the number of defective items produced by the machine, and let Y denote the number of nondefective items produced by the machine. Show that X and...

Continuation of Exercise 5-30. Let X and Y denote the number of bits with high and moderate distortion out of the three transmitted, respectively. Determine the following: (a) The probability...

Refer to the previous exercise. Now let x = number of classes skipped and y = college GPA. a. Construct a scatter-plot. Does the association seem to be positive or negative? b. Find the prediction...

The Externality when fishing in the Commons: In exercise 21.6, we showed that free access to a fishing lake causes overfishing because fishermen will continue to fish until the cost of inputs (i.e....

Let X and Y be independent random variables with uniform densities in [0, 1]. Let Z = X + Y and W = X Y. Find (a) p (X, Y ) (see Exercise 18). (b) p (X,Z). (c) p (Y,W). (d) p (Z,W).