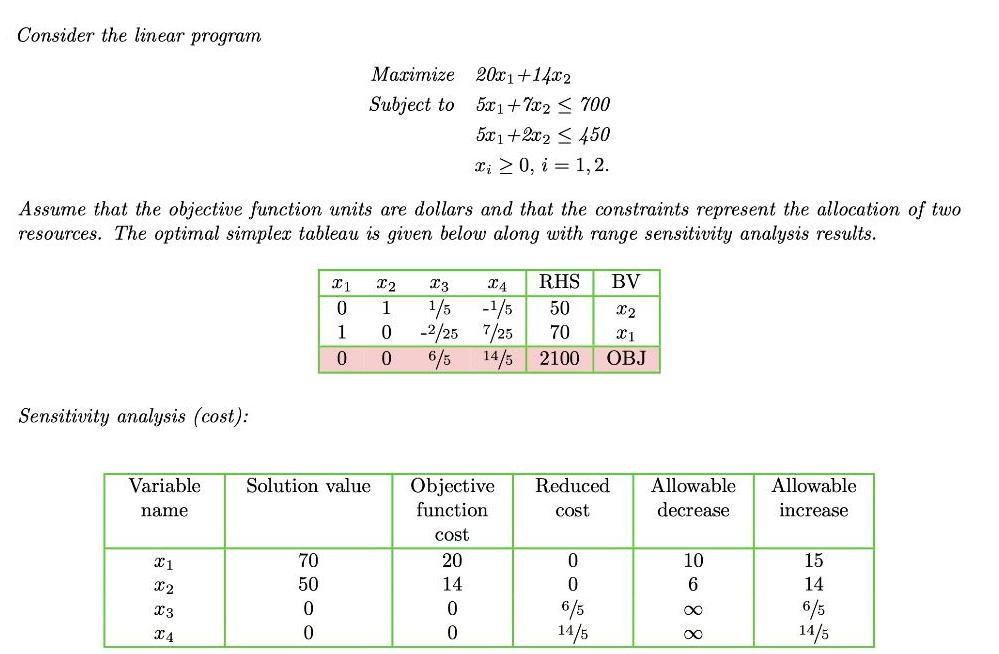
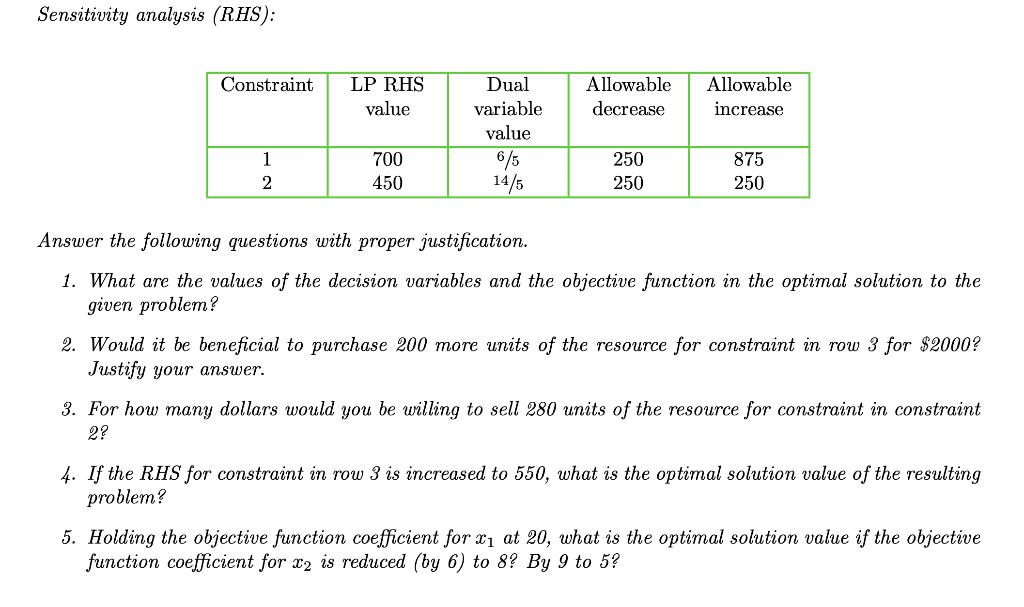
Consider the linear program Maximize 20x1+14x2 Subject to 5x1+ 7x2 < 700 5x1+2x2 < 450 Li 2 0, i = 1,2. Assume that the objective function units are dollars and that the constraints represent the allocation of two resources. The optimal simplex tableau is given below along with range sensitivity analysis results. X4 RHS BV -1/5 -2/25 7/25 6/5 1 1/5 50 x2 1 70 0. 14/5 2100 OBJ Sensitivity analysis (cost): Variable Solution value Reduced Allowable Objective function Allowable nam cost decrease increase cost 70 20 10 15 x2 50 14 6 14 6/5 14/5 6/5 14/5 X3 X4 2o 8 8 Sensitivity analysis (RHS): Constraint LP RHS Dual Allowable Allowable value variable decrease increase value 6/5 14/5 1 700 250 875 2 450 250 250 Answer the following questions with proper justification. 1. What are the values of the decision variables and the objective function in the optimal solution to the given problem? 2. Would it be beneficial to purchase 200 more units of the resource for constraint in row 3 for $2000? Justify your answer. 3. For how many dollars would you be willing to sell 280 units of the resource for constraint in constraint 2? 4. If the RHS for constraint in row 3 is increased to 550, what is the optimal solution value of the resulting problem? 5. Holding the objective function coefficient for x1 at 20, what is the optimal solution value if the objective function coefficient for x2 is reduced (by 6) to 8? By 9 to 5?