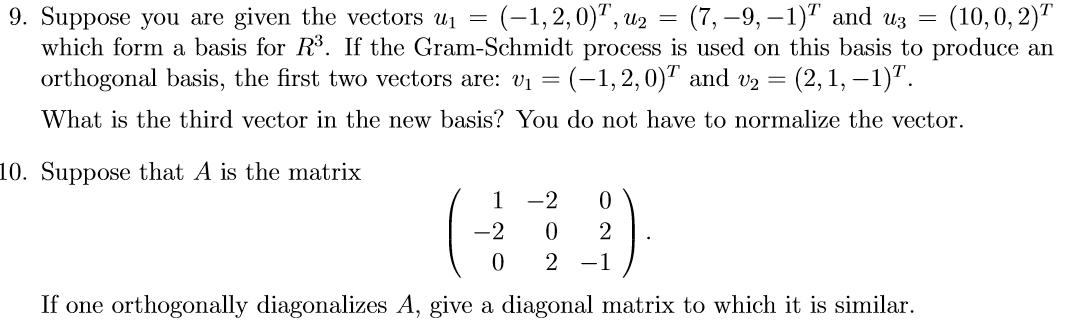
9. Suppose you are given the vectors u = (-1,2,0), u , U = (7,-9, -1) and u3 = (10, 0, 2) which form a basis for R. If the Gram-Schmidt process is used on this basis to produce an orthogonal basis, the first two vectors are: v = (-1,2,0) and v = (2,1, -1). What is the third vector in the new basis? You do not have to normalize the vector. 10. Suppose that A is the matrix 1 -2 0 -2 0 2 0 2 -1 If one orthogonally diagonalizes A, give a diagonal matrix to which it is similar.