Question: Activity 20 - Properties of Functions 6. If function f is onto, a. Ca n the domain have more elements than the codomain? b. C

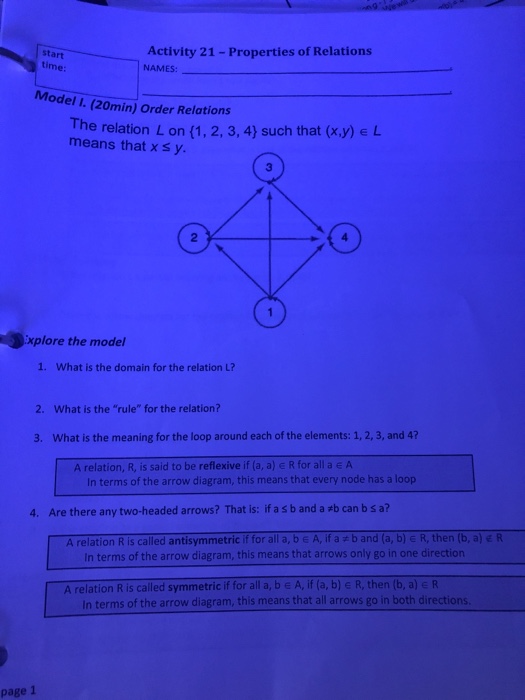
Activity 20 - Properties of Functions 6. If function f is onto, a. Ca n the domain have more elements than the codomain? b. C an the codomain have more elements than the domain? 7. If function f is one-to-one, c. Can the domain have more elements than the codomain? d. Can the codomain have more elements than the domain? 8. If function f is invertible, e. Can the domain have more elements than the codomain? f. Can the codomain have more elements than the domain? THEOREM Z Let f:A >B be a function, where A and B are finite sets of sizes m and n, respectively If f is one-to-one then msn . If f is onto, then m2n . If f is invertible, then m n Application: For each of the following functions, decide if it is one-to-one, onto, invertible or none of these 1. a. f: Q-Q with rule f(x) 3x+ 1 b. f QQ+ with rule fix)- 7x+ 5 c. : N- N with rule f(x) is the closest value for x

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

A company produces two (2) products, "Minx" and "Winx". The following sales forecast for both products was decided on for the financial year January 1, 2015 to December 31, 2015: Details Period1...

Activity 20 - Properties of Functions Critical Thinking se arrow diagrams tell if the function is onto, one-to-one and invertible. If not te ll why it is not Onto? 2 One-to-one? Invertible? 5. Onto?...

What is the natural meaning for a pair to be in this new relation,t e Definition-Composition of relations Given relation R from A to B and relation S from 8 to C, there is a relation S- R from A to C...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

Module 07 Short Answer Assignment - Functions, Domains, Ranges, 1-1, Onto - Answer Key Each graph represents a relation (A) F : X Y , that may also be a function. (B) X Y 1 (C) X (D) Y X Y 1X aY 1 a...

Microkernel operating systems aim to address perceived modularity and reliability issues in traditional "monolithic" operating systems. (i) Describe the typical architecture of a microkernel...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

A solid piece of lead has a mass of 23.94 g and a volume of 2.10 cm3. From these data, calculate the density of lead in SI units (kg/m3)

Does a firms price equal the minimum of average total cost in the short run, in the long run, or both? Explain.

Private currencies _ _ _ _ _ _ _ _ _ , but _ _ _ _ _ _ _ _ . Question 4 5 options: arise if the sovereign currency is not fulfilling a demand; the state consistently adopts the innovations of the...

Vanessa wants to buy a condo that costs $300,000 on April 1, 2020. She is excited as she has always rented. Her Net Worth statement shows: Description Fair Market Value Savings account $40,000...

KEY QUESTION The following are production possibilities tables for China and the United States. Assume that before specialization and trade the optimal product mix for China is alternative B and for...

KEY QUESTION True or False? U.S. exports create a demand for foreign currencies; foreign imports of U.S. goods create a supply of foreign currencies. Explain. Would a decline in U.S. consumer income...

What factors account for the rapid growth of world trade since the Second World War? Who are the major players in international trade today? Besides Japan, what other Asian nations play significant...