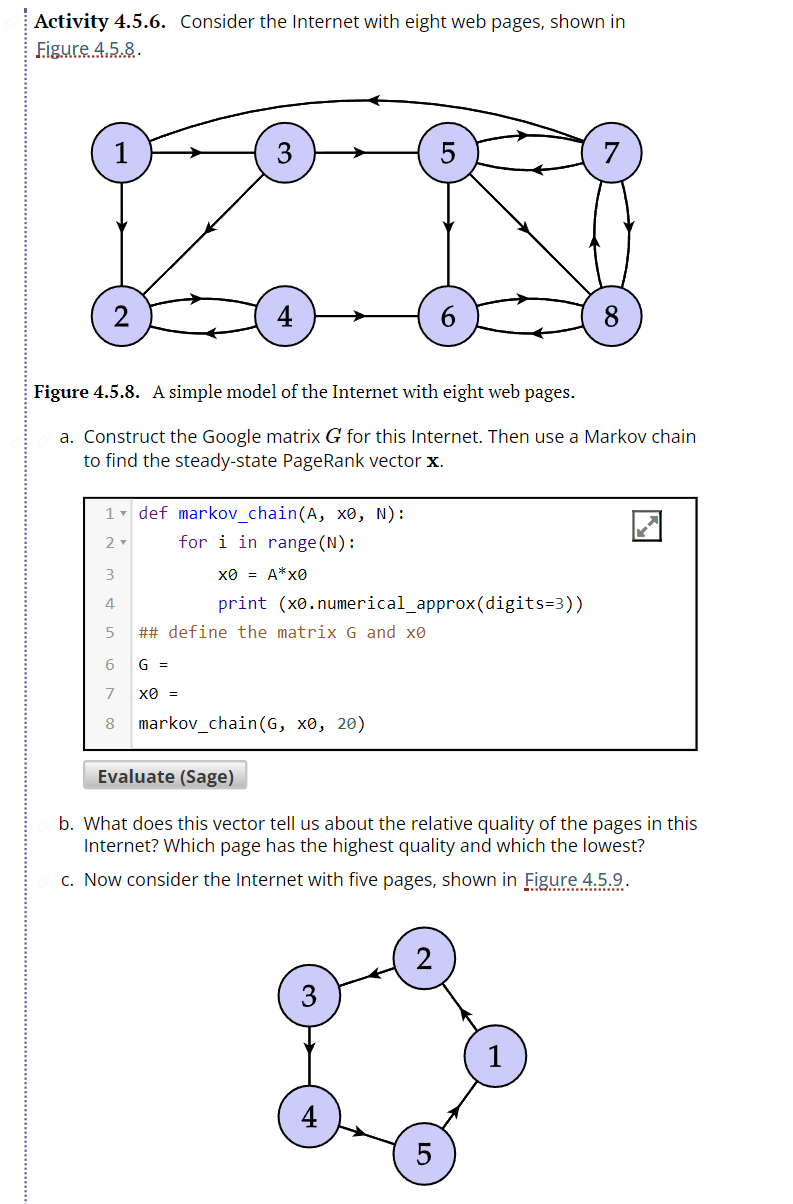
Activity $4\mathrm{.}5\mathrm{.}6.$ Consider the Internet with eight web pages, shown in Figure $4\mathrm{.}5\mathrm{.}8.$

Figure $4\mathrm{.}5\mathrm{.}8.$ A simple model of the Internet with eight web pages.

a$.$ Construct the Google matrix $\backslash ($ G $\backslash )$ for this Internet. Then use a Markov chain to find the steady$-$state PageRank vector $\backslash (\backslash$mathbf$\{$x$\}\backslash ).$

$```$

def markov$\_$chain$($A$,$ x$0,$ N$)$:

for i in range$($N$)$:

x$0=$ A$*$x$0$

print $($x$0.$numerical$\_$approx$($digits$=3))$

## define the matrix G and x$0$

G $=$

x$0=$

markov$\_$chain$($G$,$ x$0,20)$

$```$

b$.$ What does this vector tell us about the relative quality of the pages in this Internet? Which page has the highest quality and which the lowest? Figure $4\mathrm{.}5\mathrm{.}9.$ A model of the Internet with five web pages.

What happens when you begin the Markov chain with the vector $\backslash (\backslash$mathbf$\{$x$\}\_\{0\}=\backslash$left$[\backslash$begin$\{$array$\}\{$l$\}1\backslash \backslash 0\backslash \backslash 0\backslash \backslash 0\backslash \backslash 0\backslash$end$\{$array$\}\backslash$right$]\backslash )?$ Explain why this behavior is consistent with the Perron$-$

Frobenius theorem.

d$.$ What do you think the PageRank vector for this Internet should be$?$ Is any one page of a higher quality than another?

e$.$ Now consider the Internet with eight web pages, shown in Figure$\mathrm{.}4\mathrm{.}5\mathrm{.}10.$

Figure $4\mathrm{.}5\mathrm{.}10.$ Another model of the Internet with eight web pages.

Notice that this version of the Internet is identical to the first one that we saw in this activity, except that a single link from page $7$ to page $1$ has been removed. We can therefore find its Google matrix $\backslash ($ G $\backslash )$ by slightly modifying the earlier matrix.

What is the long$-$term behavior of a Markov chain defined by $\backslash ($ G $\backslash )$ and why is this behavior not desirable? How is this behavior consistent with the Perron$-$Frobenius theorem?

The Perron$-$Frobenius theorem Theorem..$\mathrm{.}4\mathrm{.}5\mathrm{.}6$ tells us that a Markov chain $\backslash (\backslash$mathbf$\{$x$\}\_\{$k$+1\}=$G $\backslash$mathbf$\{$x$\}\_\{$k$\}\backslash )$ converges to a unique steady$-$state vector when the matrix $\backslash ($ G $\backslash )$ is positive. This means that $\backslash ($ G $\backslash )$ or some power of $\backslash ($ G $\backslash )$ should have only positive entries. Clearly, this is not the case for the matrix formed from the Internet in Figure$\mathrm{.}4\mathrm{.}5\mathrm{.}9.$

We can understand the problem with the Internet shown in Figure. $4\mathrm{.}5\mathrm{.}10$ by adding a box around some of the pages as shown in Figure $4\mathrm{.}5\mathrm{.}5\mathrm{.}11.$ Here we see that the pages outside of the box give up all of their PageRank to the pages inside the box. This is not desirable because the PageRanks of the pages outside of the box are found to be zero. Once again, the Google matrix $\backslash ($ G $\backslash )$ is not a positive matrix.

Figure $4\mathrm{.}5\mathrm{.}11.$ The pages outside the box give up all of their PageRank to the pages inside the box.

Google solves this problem by slightly modifying the Google matrix $\backslash ($ G $\backslash )$ to obtain a positive matrix $\backslash ($ G$^\{\backslash$prime$\}\backslash ).$ To understand this, think of the entries in the Google matrix as giving the probability that an Internet user follows a link from one page of another. To create a positive matrix, we will allow that user to randomly jump to any other page on the Internet with a small probability.

To make sense of this, suppose that there are $\backslash ($ N $\backslash )$ pages on our internet. The matrix