Activity 4has fourproblems. For each problem, show all work.

Please complete all problems.

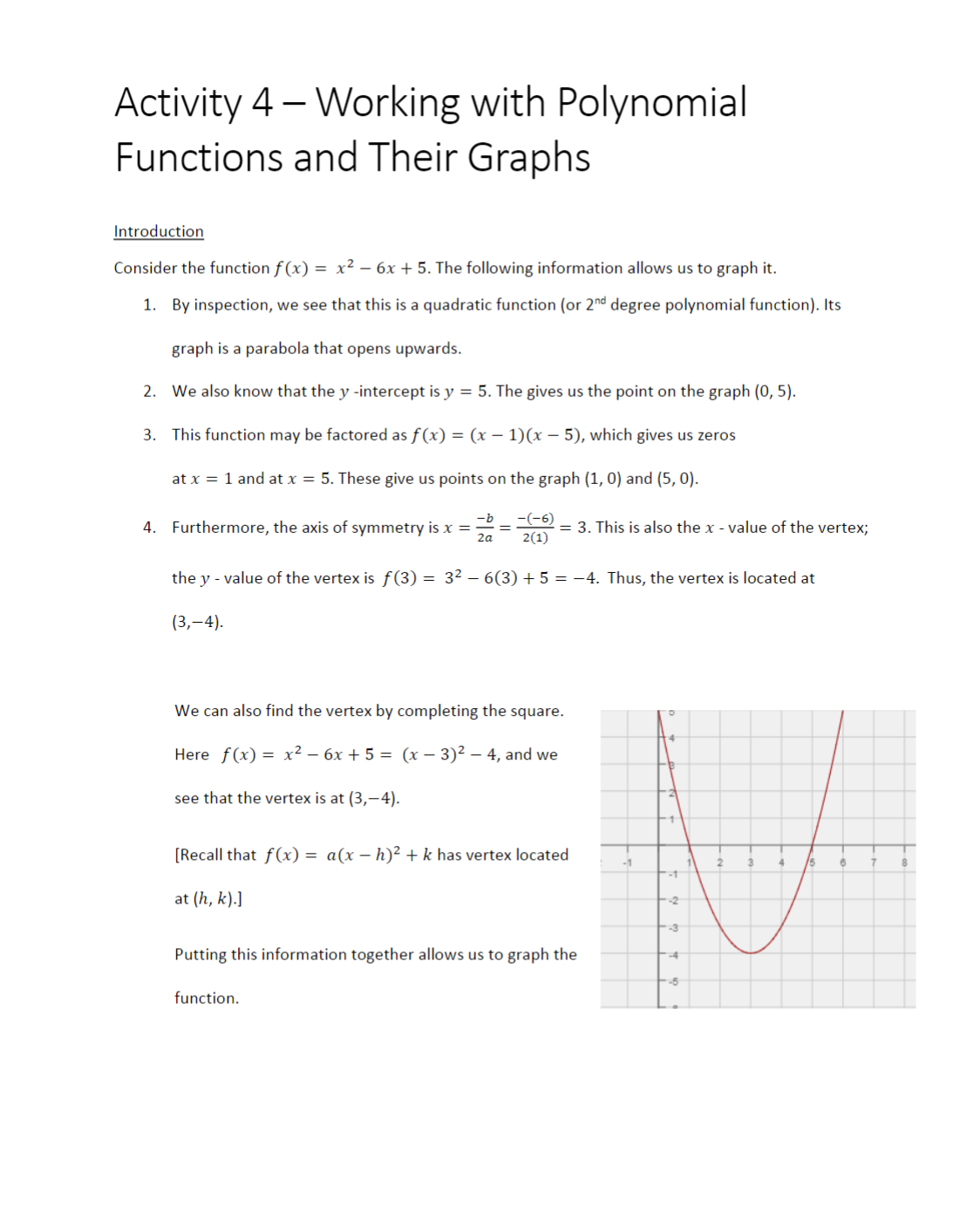
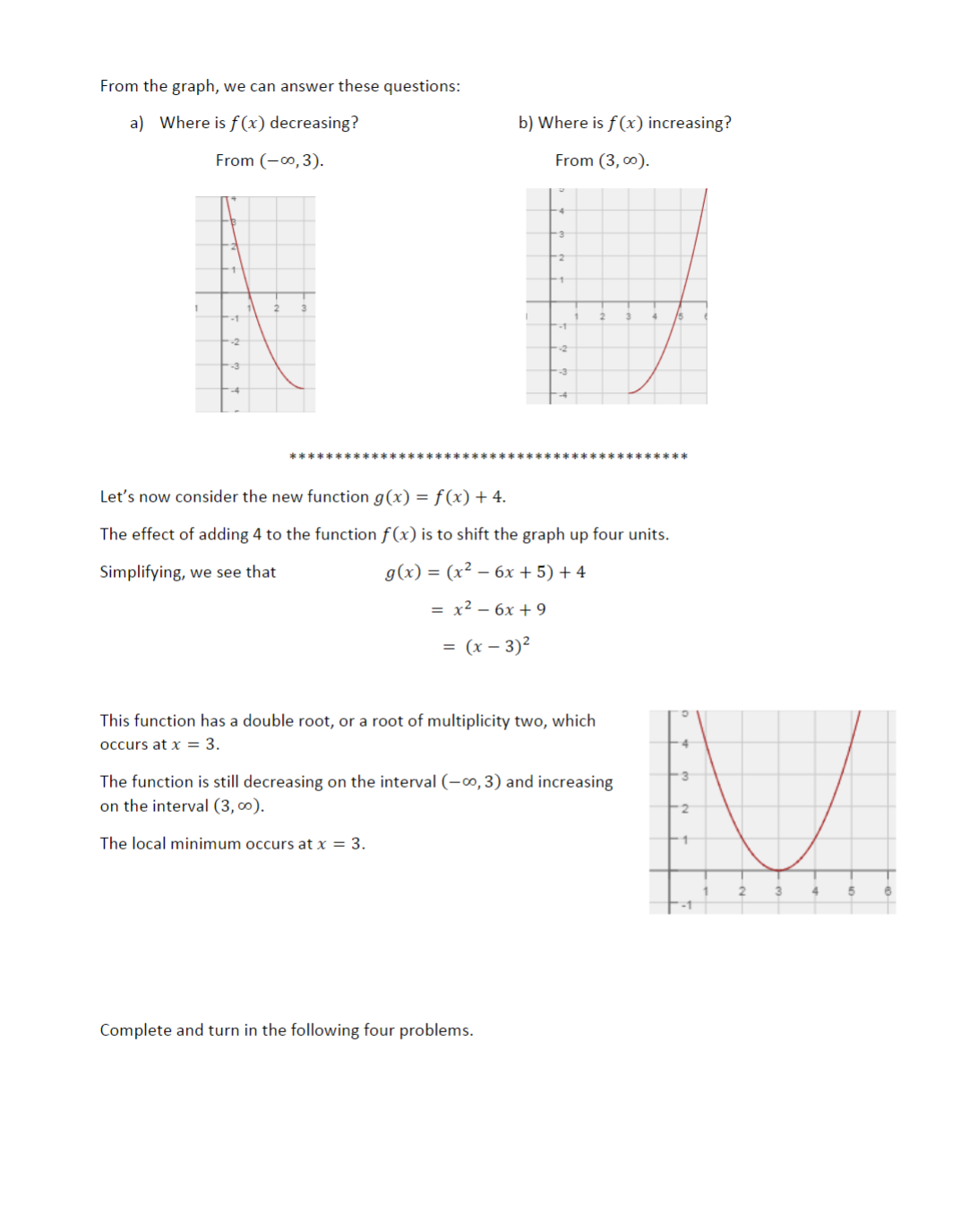
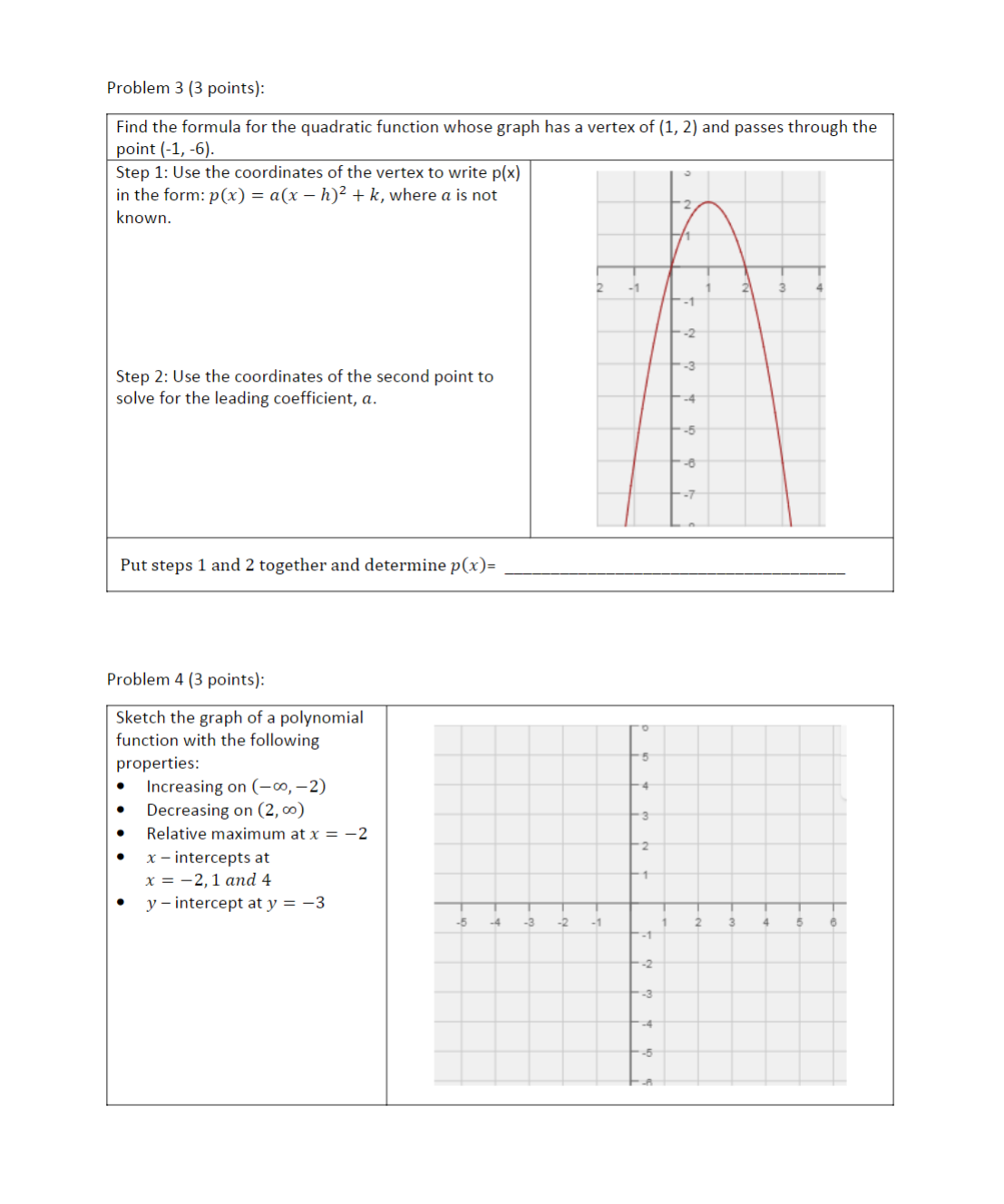
Activity 4 Working with Polynomial Functions and Their Graphs Introduction Consider the function f(x) = x? 6x + 5. The following information allows us to graph it. 1. By inspection, we see that this is a quadratic function (or 2 degree polynomial function). Its graph is a parabola that opens upwards. 2. We also know that the y -intercept is y = 5. The gives us the point on the graph (0, 5). 3. This function may be factored as f(x) = (x 1)(x 5), which gives us zeros at x = 1 and at x = 5. These give us points on the graph (1, 0) and (5, 0). % 3 - _b . (-86) 4. Furthermore, the axis of symmetry is x = %= 20 = 3. Thisis also the x - value of the vertex; the y - value of the vertex is f(3) = 32 6(3) + 5 = 4. Thus, the vertex is located at (3,4). We can also find the vertex by completing the square. Here f(x)= x> -6x+5= (x3)24,and we see that the vertex is at (3,4). [Recall that f(x) = a(x h)? + k has vertex located at (h, k).] Putting this information together allows us to graph the function. From the graph, we can answer these questions: a) Where is f(x) decreasing? b) Where is f (x) increasing? From (-0o, 3 ) . From (3, 00). 2 * * *** * * Let's now consider the new function g(x) = f (x) + 4. The effect of adding 4 to the function f (x) is to shift the graph up four units. Simplifying, we see that g (x) = (x2 - 6x + 5)+4 = x2 - 6x + 9 = (x -3)2 This function has a double root, or a root of multiplicity two, which occurs at x = 3. The function is still decreasing on the interval (-co, 3) and increasing on the interval (3, co). The local minimum occurs at x = 3. Complete and turn in the following four problems.Problem 1 (2 points): Sketch a cubic function (third degree polynomial function) y = p(x) where p(x) > 0 on the intervals (,2) and (4,6). Then determine a formula for your function. Sketch: Formula: | p(x)= Problem 2 (2 points): Sketch a cubic function (third degree polynomial function) y = p(x) with two distinct zeros at x = 1 and x = 4 and a local maximum at x = 4. Then determine a formula for your function. [Hint: you will have one double root.] Sketch: Problem 3 (3 points): Find the formula for the quadratic function whose graph has a vertex of (1, 2) and passes through the point (-1, -6). Step 1: Use the coordinates of the vertex to write p(x) in the form: p(x) = a(x h)? + k, where a is not known. Step 2: Use the coordinates of the second point to solve for the leading coefficient, a. Put steps 1 and 2 together and determine p(x)= Problem 4 (3 points): Sketch the graph of a polynomial function with the following properties: Increasing on (w,2) Decreasingon (2, ) s Relative maximum at x = 2 * X intercepts at x==2,1land 4 y interceptaty = =3