Additional question, what would be the slack time for each of the following:

A=

B=

C=

D=

E=

F=

G=

PRIOR RESULTS below:

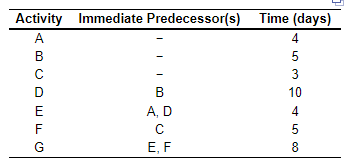
Roger Ginde is developing a program in supply chain management certification for managers. Ginde has listed a number of activities that must be completed before a training program of this nature could be conducted. The activities, immediate predecessors, and times appear in the accompanying table:

The critical activities for the leadership training program development project are? (see options below chart)

Which is the Answer:

C - F - G

A - E - G

OR

B - D - E - G

Show transcribed data

Expert Answer

This solution was written by a subject matter expert. It's designed to help students like you learn core concepts.

Step-by-step

1st step

All steps

Answer only

Step 1/2

To determine the critical path for the leadership training program development project, we need to find the longest path through the network of activities. The critical path is the sequence of activities that must be completed on time to complete the entire project on time. It represents the shortest time in which the project can be completed.

.

Explanation:

We can start by calculating the earliest start and finish times for each activity using the forward pass method. Then, we calculate the latest start and finish times using the backward pass method. Activities that have the same earliest start and finish times on the critical path are part of the critical path.

Here's the calculation for the critical path:

Start with activities A, B, and C since they have no predecessors.

A: ES = 0, EF = 4

B: ES = 0, EF = 5

C: ES = 0, EF = 3

Activity D depends on B, so its ES is the EF of B.

D: ES = 5, EF = 5 + 10 = 15

Activity E depends on A and D. Its ES is the maximum of the EFs of A and D.

E: ES = max(4, 15) = 15, EF = 15 + 4 = 19

Activity F depends on C, so its ES is the EF of C.

F: ES = 3, EF = 3 + 5 = 8

Activity G depends on E and F. Its ES is the maximum of the EFs of E and F.

G: ES = max(19, 8) = 19, EF = 19 + 8 = 27

Step 2/2

Now, we calculate the latest start and finish times (LS and LF) using the backward pass method:

For activity G, since it's the last activity, LS = LF = EF = 27.

For activity F, LS = LF - Duration = 27 - 8 = 19.

For activity E, LS = LF - Duration = 19 - 4 = 15.

For activity D, LS = LF - Duration = 15 - 10 = 5.

For activities A, B, and C, LS = LF - Duration = 4, 5, and 3, respectively.

Explanation:

Now, we compare the ES and LS values for each activity. If ES equals LS, the activity is on the critical path:

Activity A: ES = 0, LS = 4 (not on the critical path)

Activity B: ES = 0, LS = 5 (not on the critical path)

Activity C: ES = 0, LS = 3 (not on the critical path)

Activity D: ES = 5, LS = 5 (on the critical path)

Activity E: ES = 15, LS = 15 (on the critical path)

Activity F: ES = 3, LS = 19 (not on the critical path)

Activity G: ES = 19, LS = 27 (not on the critical path)

Final answer

Therefore, the critical path for the leadership training program development project is:

B - D - E - G

\\begin{tabular}{ccc} \\hline Activity & Immediate Predecessor(s) & Time (days) \\\\ \\hline A & - & 4 \\\\ B & - & 5 \\\\ C & - & 3 \\\\ D & B & 10 \\\\ E & A, D & 4 \\\\ F & C & 5 \\\\ G & E, F & 8 \\\\ \\hline \\end{tabular}