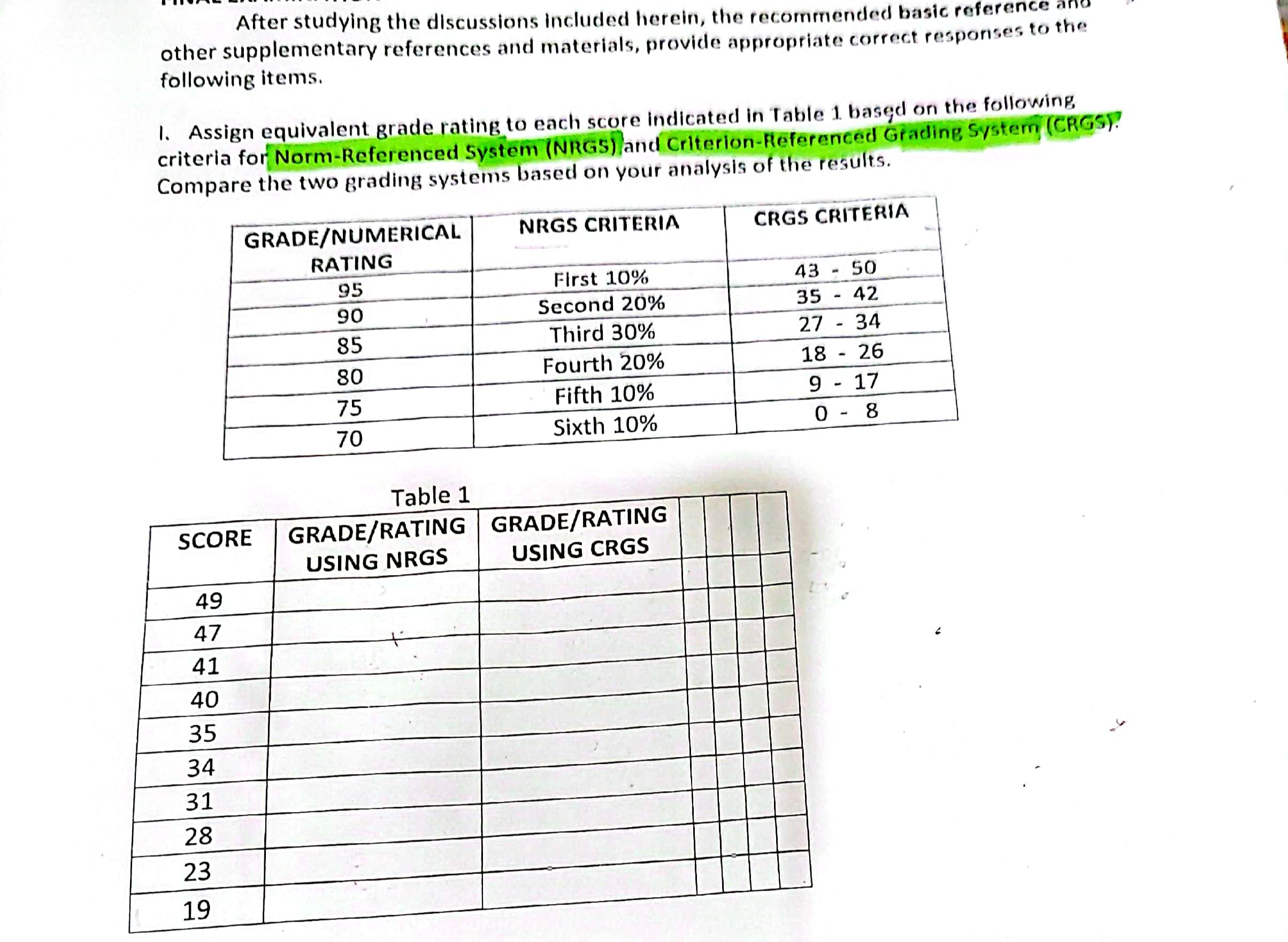
After studying the discussions included herein, the recommended basic reference and other supplementary references and materials, provide appropriate correct responses to the following items. I. Assign equivalent grade rating to each score indicated in Table 1 based on the following criteria for Norm-Referenced System (NRGS) and Criterion-Referenced Grading System (CRGS). Compare the two grading systems based on your analysis of the results. GRADE/NUMERICAL NRGS CRITERIA CRGS CRITERIA RATING 95 First 10% 43 - 50 90 Second 20% 35 - 42 85 Third 30% 27 - 34 80 Fourth 20% 18 - 26 75 Fifth 10% 9 - 17 70 Sixth 10% 0 - 8 Table 1 SCORE GRADE/RATING GRADE/RATING USING NRGS USING CRGS 49 47 41 40 35 34 31 28 23 19roduction Assessment of student performance is essentially knowing how the student is progressing in a course (and incidentally, how a teacher is also performing with respect to the teaching process.) The first step in assessment is, of course testing, followed by a decision to grade the performance of the student. Grading. therefore, is the next step after testing. Grading system had been evolved in different school systems all over the world. With the implementation of the K to 12 Basic Education Curriculum, however, student's performance is expressed in terms of level of proficiency. It is clear that there appears to be a need to convert a raw score values into corresponding standard grading system. This chapter is concerned with the underlying philosophy and mechanics of converting raw score values into standard grading formats. B. Norm- Referenced Grading The most commonly used grading system falls under the category of norm- referenced grading. Norm- reference grading refers to a grading system wherein a student's grade is placed in relation to the performance of a group. A grade 80% means that the student performed better than or same as 80% of the class. The following example shows some of the difficulties associated with norm- referenced grading. Example: Consider the following two sets of scores in an English 1 class for two sections of ten students each: A= (30, 40, 50, 55, 60, 65, 70, 75, 80, 85) B= (60, 65, 70, 75, 80, 85, 90, 90 95, 100) In the first class, the students who get a raw score of 75 would get a grade of 80% while in the second class, the same grade of 80% would correspond to a raw score of 90. Indeed, if the test used for the two classes are the same, it would be a rather "unfair" system of grading. A wise student would opt to enroll in class A since it is easier to get higher grades in that class than in the other class (class B). The previous example illustrates one difficulty with using a norm- referenced grading system. This problem is called the problem of equivalency. As we have seen, norm- referenced grading system are based a pre- established formula regarding the percentage or ratio of students within a whole class will be assigned each grade or mark. In norm- referenced grading, the students, while they may word individually, are actually in competition to achieve a standard of performance that will classify them into the desired grade range. A student or pupil who happens to enroll in a class of gifted students in Mathematics will find that the norm- referenced grading system is rather worrisome. For example, a teacher may establish a grading policy wher the top 15 percent of the students will receive a mark of excellent or outstanding, which in class 100 enroll students will 15 persons. Such a grading policy is listed below: 1.0 (Excellent) Top 15% of the class 1.50 (Good) = Next 15% of the class 2.0 (Average, Fair) Next 45% of the class 3.0 (Poor, Pass) Next 15% of the class 5.0 (Failure) Bottom 10% of the class Norm- referenced systems are most often used for screening selected student populations in conditions where it is known that not all students can advance due to limitations such as available plac or other controlling factors. For example, in the Philippine setting, since not all high school students ca actually advance to college or university level because of financial constraints, the norm- referenced g system can be applied. Example in a class of 100 students, the mean score in a test is 70 with a standard deviation of Construct a norm- referenced grading table that would have seven grade scales and such that student between plus or minus one standard deviation from the mean receives an average grade. Solution: The following intervals of raw scores to grade equivalent are computed. Raw Score Grade Equivalent Percentage Below 55 Fail 1%55-60 Marginal Pass 61-65 Pass 11% 66-75 Average 58% 75-80 Above Average 1.1% 81-85 Very Good 4% Above 85 Excellent 1% When a teacher is faced with a particular bright class, most of the time, he does not penalize good students for having the bad luck to enroll in a class with a cohort of other very capable students even if the grading system says he should fail a certain percentage of the class. A teacher would reduce the mean grade for a class when he observes a large proportion of poor performing students just to save them from failure. A serious problem with norm- referenced grading is that, no matter what the class level of knowledge and ability. Norm- referenced grading and evaluation is often used to weed out the students for limited places in selective educational programs. A more subtle problem with norm- referenced grading is that a strict correspondence between the evaluation method used and the course instructional goals is not necessary to yield the required grade distribution. The specific learning objectives of norm- referenced classes are often kept hidden, in part out of concern that instruction not "give away" the test or the teacher's priorities, since this might tend skew the curve. C. Criterion- Referenced Grading Criterion- referenced grading systems are based on a fixed criterion measure. There is a fixed target and the students must achieve that target in order to obtain a passing grade in a course regardless of how the other students in the class perform. For example, in a class of 100 students using the table below, no one might get grade of excellent if no one scores 98 above or 85 above depending on the criterion used. There is no fixed percentage of students who are expected to get the various grades in the criterion- referenced grading system. 1.0 (Excellent) = 98- 100 or 85-100 1.5 (Good) = 88-97 or 80-84 2.0 (Fair) = 75-87 or 70-79 3.0 (Poor/ Pass) = 65-74 or 60-69 5.0 (Failure) = below 75 or below 60 Criterion- referenced systems are often used in situations where the teachers are agreed on the mean of a "standard of performance" in a subject but the quality of the students is unknown or uneven, where th work involves student collaboration or teamwork, and where there is no external driving factor such as needing a systematically reduce a pool of eligible students. Note that in criterion- referenced system, students can help a fellow student in a group work withou necessarily worrying about lowering his grade in that course. This is because the criterion- referenced grad ystem does not require the mean (of the class) as basis for distributing grades among the students