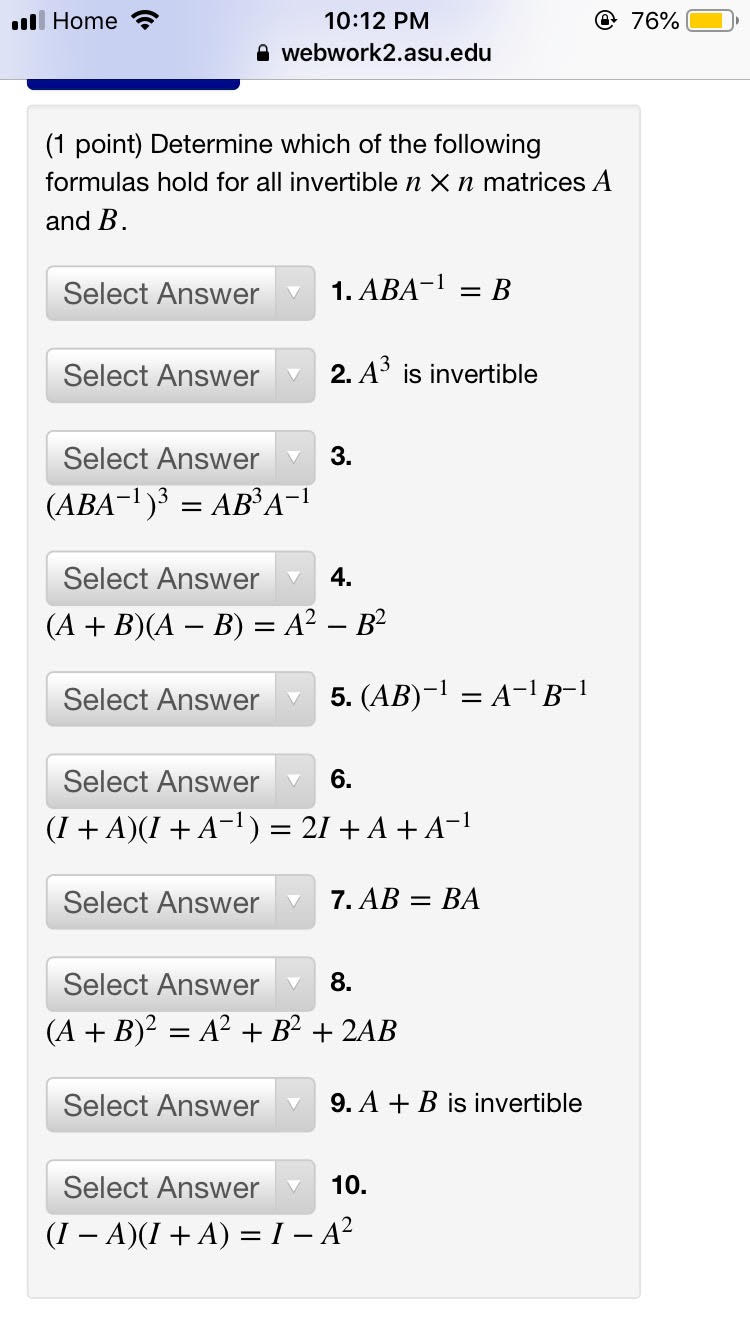
al Home - 10:12 PM @ 76% a webwork2.asu.edu (1 point) Determine which of the following formulas hold for all invertible n X n matrices A and B. Select Answer V 1. ABA- = B Select Answer V 2. A' is invertible Select Answer V 3. (ABA-1)3 = ABBA- Select Answer V 4. (A + B)(A - B) = A2 - B2 Select Answer V 5. (AB)-1 = A-1 B-1 Select Answer V 6. (I + A)(I + A-] ) = 2/ + A +A-l Select Answer V 7. AB = BA Select Answer V 8. (A + B)2 = A2 + B2 + 2AB Select Answer V 9. A + B is invertible Select Answer 10. (1 - A)(I + A) = 1 - A2al Home - 10:12 PM @ 76% a webwork2.asu.edu Previous Problem Problem List Next Problem (1 point) A square matrix is called a permutation matrix if it contains the entry 1 exactly once in each row and in each column, with all other entries being 0. All permutation matrices are invertible. Find the inverse of the following permutation matrix 0 0 0 O A = O 1 0 0 O 0 O O A- = Note: You can earn partial credit on this problem. Preview My Answers Submit Answersal Home - 10:11 PM @ 76% a webwork2.asu.edu (1 point) Consider the following two systems. (a) -4x - 4y 4x - 9y = -3 (b) -4x - 4y = -2 4x - 9y = (i) Find the inverse of the (common) coefficient matrix of the two systems. A-I : (ii) Find the solutions to the two systems by using the inverse, i.e. by evaluating A- B where B represents the right hand side (i.e. B = -2 -3 for system (a) and B = for system (b)). Solution to system (a): x = Solution to system (b): x =