Question: Algorithm 6.7.1 of the class notes is as follows: 1. We consider the matrix 4 2 -6 4 2 2 -3 1 6 -3 13

Algorithm 6.7.1 of the class notes is as follows: 1. We

Algorithm 6.7.1 of the class notes is as follows:

consider the matrix 4 2 -6 4 2 2 -3 1 6

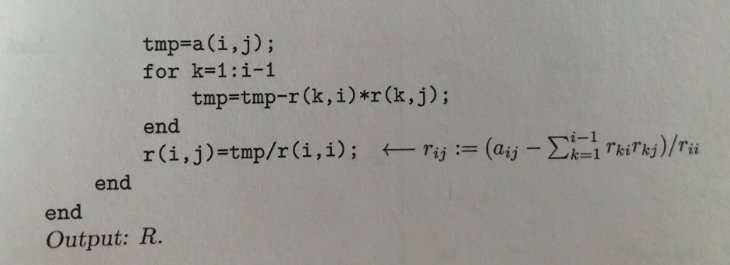
-3 13 0 4 1 0 30 E R4x4 (a) Calculate the

1. We consider the matrix 4 2 -6 4 2 2 -3 1 6 -3 13 0 4 1 0 30 E R4x4 (a) Calculate the matrix factor R of the Cholesky decomposition A RTR by using Algorithm 6.7.1 of the class notes. (b) Solve for y the lower triangular linear system Ry b where -25' 68 Then solve for x the upper triangular linear system Rz = y and check that x satisfies Ax b. (c) Using the matrix factor R of the Cholesky decomposition of A give the exact value of the determinant det(A) 1. We consider the matrix 4 2 -6 4 2 2 -3 1 6 -3 13 0 4 1 0 30 E R4x4 (a) Calculate the matrix factor R of the Cholesky decomposition A RTR by using Algorithm 6.7.1 of the class notes. (b) Solve for y the lower triangular linear system Ry b where -25' 68 Then solve for x the upper triangular linear system Rz = y and check that x satisfies Ax b. (c) Using the matrix factor R of the Cholesky decomposition of A give the exact value of the determinant det(A)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

I'm working on Question #5 (parts a and b) and do not have a good understanding of Put Warrant or Convertible Bonds. I'm able to find some information on line as to what they are, however, it is...

[ Question 6 ] Edge Detection ( 5 0 marks ) In this question, the goal is to implement a rudimentary edge detection process that uses a derivative of Gaussian, through a series of steps. For each...

Images should be more clear now. Thank you. Overview The purpose of this assignment is to broaden your understanding of deterministic finite automata and their acceptance relation. Recall that a...

The images are now bigger Overview The purpose of this assignment is to broaden your understanding of deterministic finite automata and their acceptance relation. Recall that a deterministic finite...

Graphs (Data Structures), ASAP please. A directed complete graph with 10 vertices will have 45 edges. True False A spanning tree with 10 vertices will have exactly 7 edges. True False If a spanning...

LAB 12 [1] Suppose that we have an array called list initialized as follows: (1 pts) int[] list = {-2, 8, 13, 22, 25, 25, 38, 42, 51, 103}; This would construct the following array: [0] [1] [2] [3]...

Graphs (Data Structures), ASAP please. Consider an undirected graph defined as follows: Set of vertices = {0,1, 2, 3, 4} and Set of edges = {(0, 1), (0, 2), (0,3), (0, 4), (1,3), (3, 4)} Which of the...

Specification Define a program called DFACheck which will accept as its input a pair of file names, the first of which contains a textual representation of a DFA, and the second of which contains a...

Math 400 Assignment #3 -- Numerical Integration and Differentiation 1. For the function g x e x 2 2 Due: 6am April 09, 2016 use the centered difference formula with h 101 , 102 , , 1020 to create a...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Explain why clinicians may be overly influenced by negative tests with poor sensitivity. (consider the implications of diagnostic tests that demonstrate poor sensitivity)

If the natural length of a spring is 0.5 meter, and if its takes a force of 13 newtons to keep it extended an additional 0.05 meters, find the work done in stretching the spring from its natural...

Needing a hand with the LIFO section. 1 . Based on the information given above, calculate cost of goods sold and ending inventory using the FIFO method. 2 . Calculate cost of goods sold and ending...

please try to give correct answer 5 2 3 .

Explain the difference between Job Analysis, Job Classification, and Job Evaluation.

What does Processing of an OLAP Cube accomplish?

After designing a Multidimensional Database in Visual Studio, what are the next steps that build the Database in the Analysis Services Instance? How is the build out of the Analytical Services...