Algorithms Design and Analysis

Consider the Chad algorithm to try and find the shortest paths from 1 to every other vertex. The Chad algorithm works in a way similar to Djikstras algorithm. Initially, like with Djikstras algorithm, all d[ ] values are set to infinity, then d[1] is set to 0. Where the Chad algorithm differs from Djikstras algorithm is how it selects the next vertex from the unknown vertices. Instead of next selecting the vertex which has the smallest d[ ] value (which is what Djikstras algorithm does), the Chad algorithm selects the vertices in increasing numerical order i.e. the Chad algorithm will first select the vertex 2, make this d[2] value the final d[2] value, then relax from 2, then select the vertex 3, make this d[3] value the final d[3] value, then relax from 3, and so on. You have to find a counterexample to show that the Chad algorithm does not always work correctly: (a) Show the graph G which is your counterexample. (b) Show what will be the d[ ] values printed out by the Chad algorithm. (c) Show that these are not the correct d[ ] values by showing there is some vertex v for which there is actually a better d[ ] value i.e. where the length of the shortest path to v is smaller than the d[ ] value output by the Chad algorithm i. State what is the vertex v ii. State what is the d[v] value output by the Chad algorithm iii. State what is the correct d[v] value.

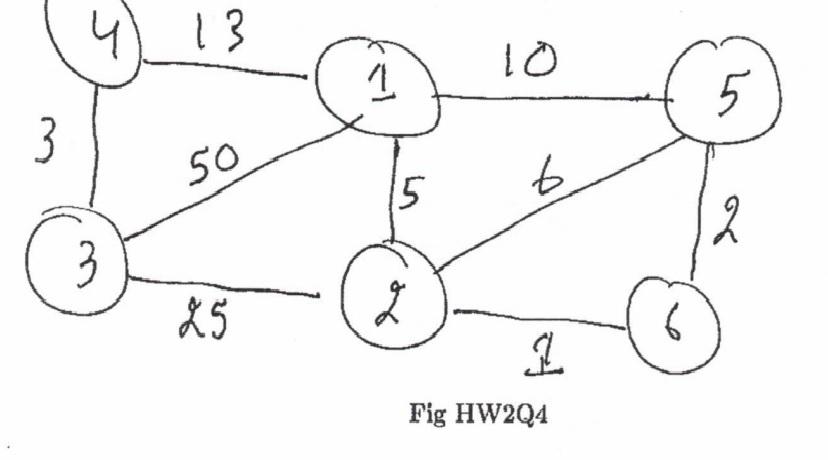
13 10 4 3 50 6 5 2 3 45 Fig HW2Q4