All the parts are complete

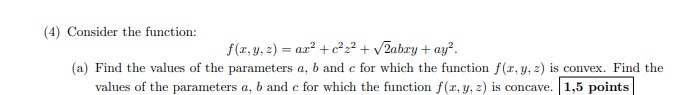
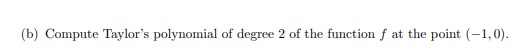
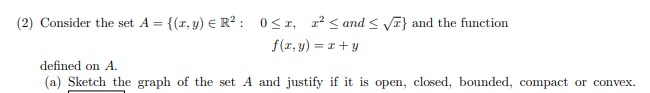
(5) Consider the function f(x, y, 2) = a + and + 2 defined on the set A= {(x,y,2) ER' :x'ty' + 227 = 4,xty =2) (a) Write the Lagrange equations for f on the set A. Compute the points that satisfy those equations and the values of the associated Lagrange multipliers. 1 point (b) Using the second order conditions, classify the critical points found in the previous part. Determine the global maxima and minima of the function f on the set A. |1 point(4) Consider the function: f(x, y, 2 ) = ax3+c323 + v2abry + ay?. (a) Find the values of the parameters a, b and c for which the function f(r, y, 2) is convex. Find the values of the parameters a, b and c for which the function f(x, y, 2) is concave. |1,5 points[11} Consider the ease when a = 1. b = 3. Does the function x, 3;, e] have a local minimum er 3 1:24:31 maximum? D,5 paints (3) Consider the function f(x, y) = rev. (a) Compute the equation of the plane tangent to the graph of the function f at the point (-1, 0, 1). 1 point(b) Compute Taylor's polynomial of degree 2 of the function f at the point (-1, 0).(2) Consider the set A = {(x,y) ER? : 0