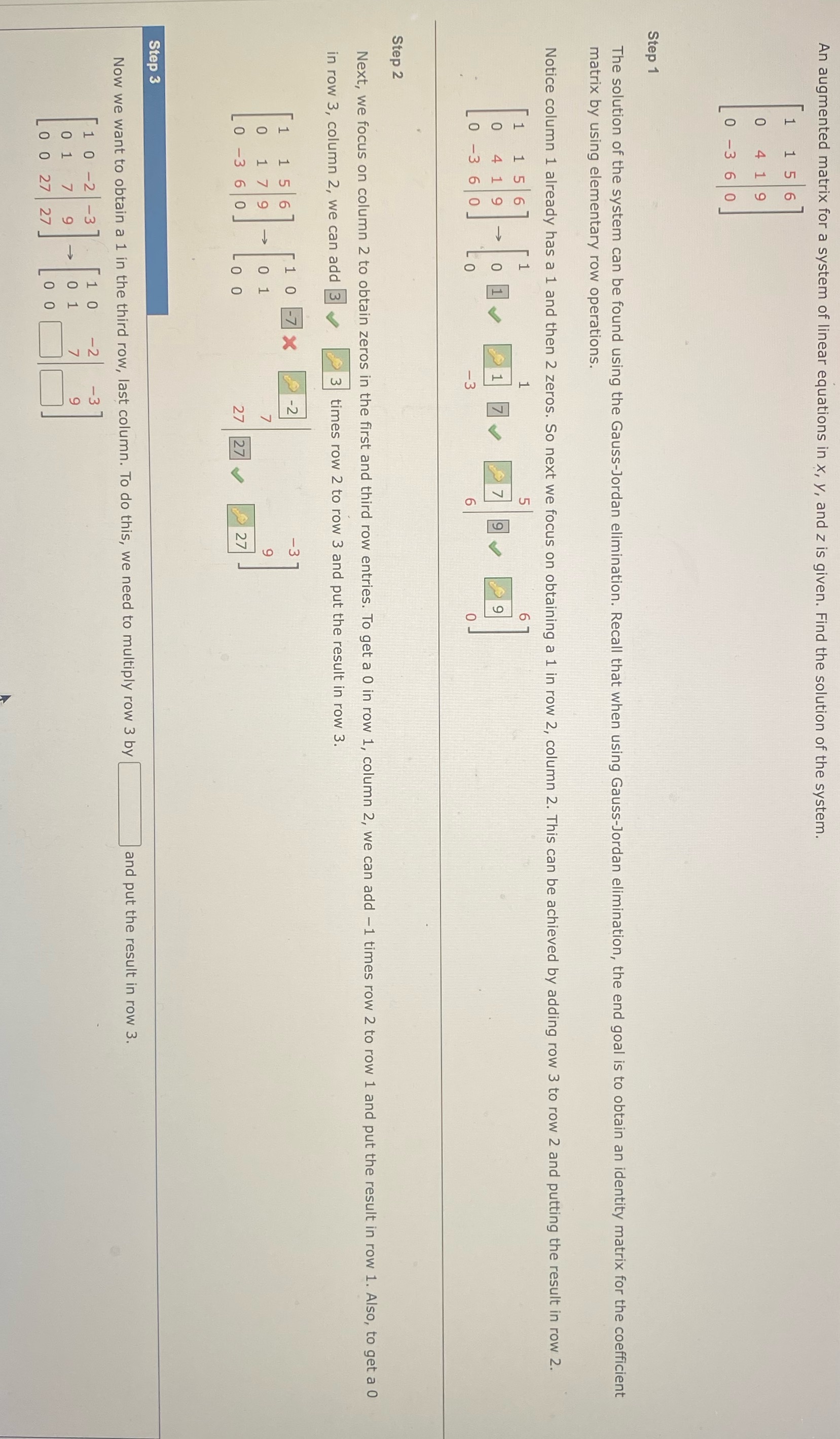
An augmented matrix for a system of linear equations in x, y, and z is given. Find the solution of the system. 1 6 0 4 9 O -36 0 Step 1 The solution of the system can be found using the Gauss-Jordan elimination. Recall that when using Gauss-Jordan elimination, the end goal is to obtain an identity matrix for the coefficient matrix by using elementary row operations. Notice column 1 already has a 1 and then 2 zeros. So next we focus on obtaining a 1 in row 2, column 2. This can be achieved by adding row 3 to row 2 and putting the result in row 2. LO O Step 2 Next, we focus on column 2 to obtain zeros in the first and third row entries. To get a 0 in row 1, column 2, we can add -1 times row 2 to row 1 and put the result in row 1. Also, to get a 0 in row 3, column 2, we can add 3 3 times row 2 to row 3 and put the result in row 3. -7 X N m 27 N Step 3 Now we want to obtain a 1 in the third row, last column. To do this, we need to multiply row 3 by and put the result in row 3