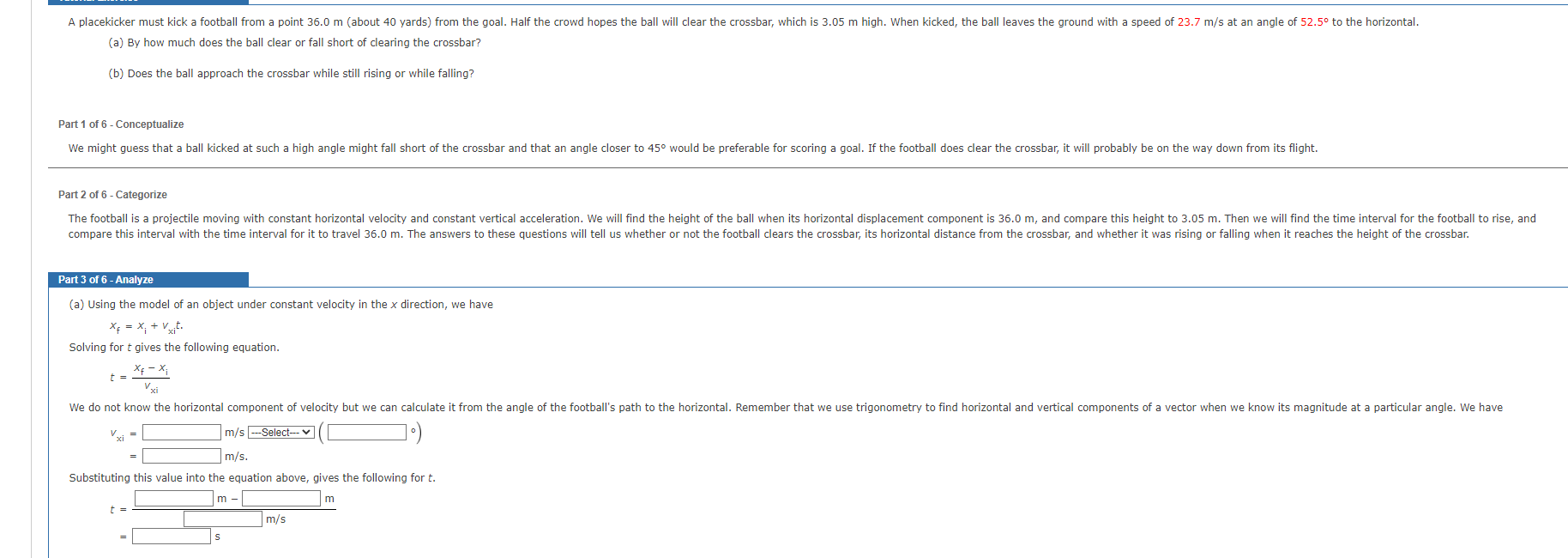
An eagle dives toward the ground with a constant velocity of 4.80 m/s at 56.0 below the horizontal. The Sun is directly overhead and casts a shadow of the eagle directly below it. What is the speed (in m/s) of its shadow on level ground? m/s Need Help? Read ItA placekicker must kick a football from a point 36.0 m (about 40 yards) from the goal. Half the crowd hopes the ball will clear the crossbar, which is 3.05 m high. When kicked, the ball leaves the ground with a speed of 23.7 m/s at an angle of 52.50 to the horizontal. (a) By how much does the ball clear or fall short of clearing the crossbar? (b) Does the ball approach the crossbar while still rising or while falling? Part 1 of 6 - Conceptualize We might guess that a ball kicked at such a high angle might fall short of the crossbar and that an angle closer to 450 would be preferable for scoring a goal. If the football does clear the crossbar, it will probably be on the way down from its flight. Part 2 of 6 - Categorize The football is a projectile moving with constant horizontal velocity and constant vertical acceleration. We will find the height of the ball when its horizontal displacement component is 36.0 m, and compare this height to 3.05 m. Then we will find the time interval for the football to rise, and compare this interval with the time interval for it to travel 36.0 m. The answers to these questions will tell us whether or not the football clears the crossbar, its horizontal distance from the crossbar, and whether it was rising or falling when it reaches the height of the crossbar. Part 3 of 6 - Analyze (a) Using the model of an object under constant velocity in the x direction, we have XF = X; +Vit. Solving for t gives the following equation. Xf - Xi Vxi We do not know the horizontal component of velocity but we can calculate it from the angle of the football's path to the horizontal. Remember that we use trigonometry to find horizontal and vertical components of a vector when we know its magnitude at a particular angle. We have m/s -Select- m/s . Substituting this value into the equation above, gives the following for t. m - Im 1m/s