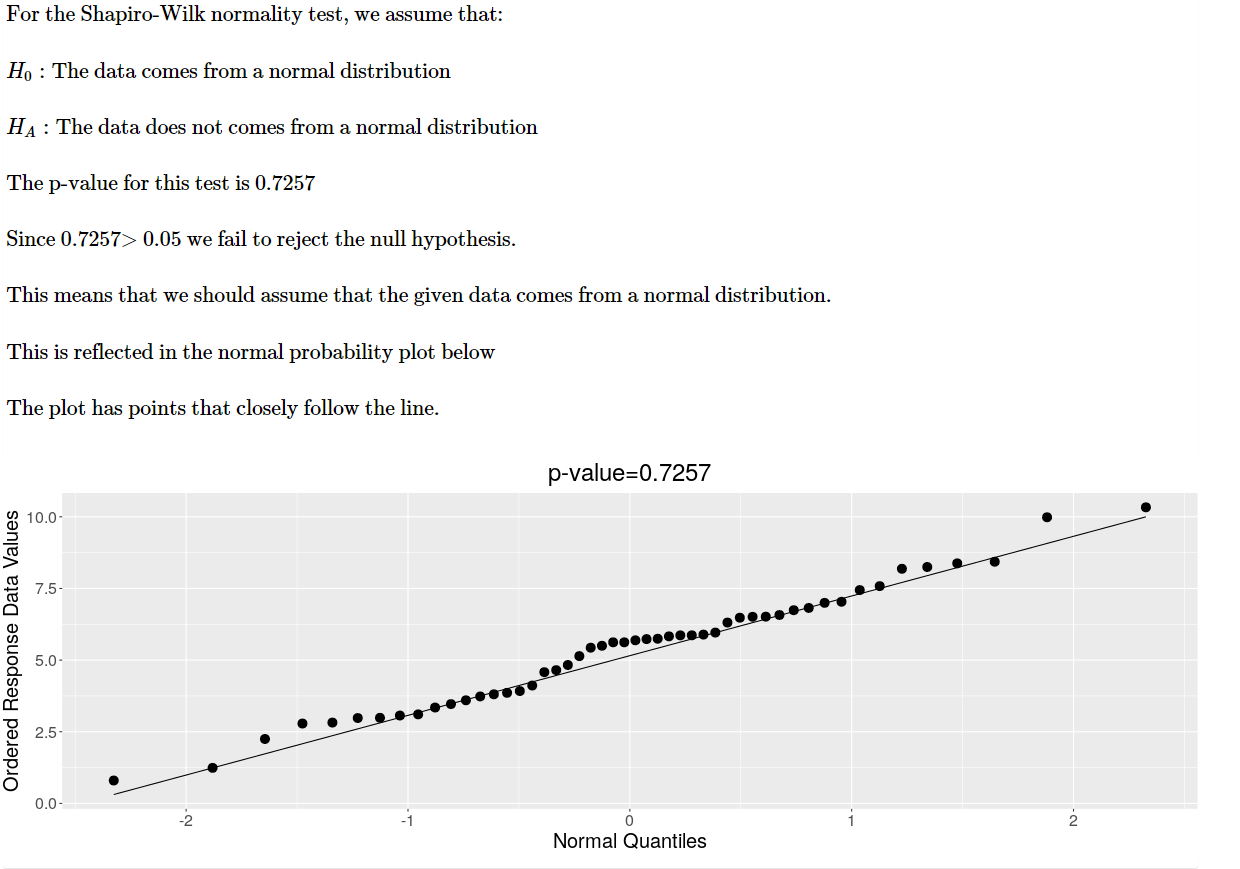
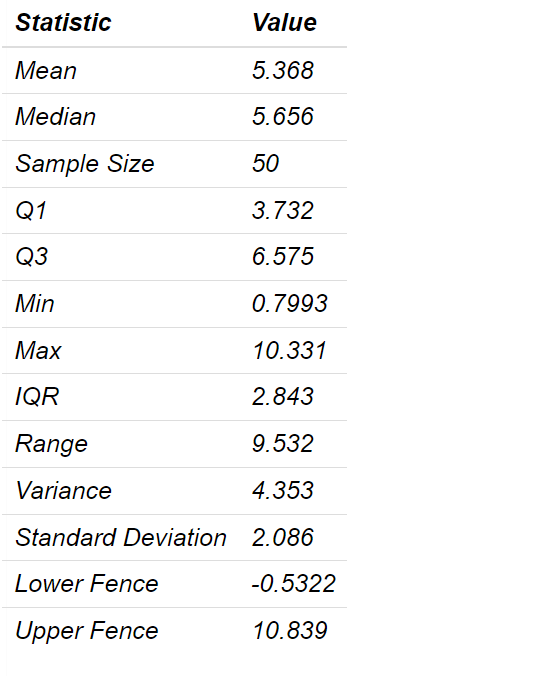
An engineer is doing a study in a manufacturing setting on the lengths of paperelips. The sample he collected is in the dataset paperclipsxlsx. Assume that the target value for the pa perelip length is 6 cm. He would like to see if this assumption still holds. a. Check to see if the data seems to come from a normal distribution 12:. Give the null and alternative hypotheses for this situation e. Determine the test statistic in this case {show work] d. L'sing t1=0.05. test the hypothesis and draw conclusions e. Give the realworld answer For the Shapiro-Wilk normality test, we assume that: H g : The data comes from a normal distribution HA : The data does not comes from a normal distribution The p-value for this test is 0.7257 Since 0.7257> 0.05 we fail to reject the null hypothesis. This means that we should assume that the given data comes from a normal distribution. This is reected in the normal probability plot below The plot has points that closely follow the line. p-value=0.7257 9 C) 5' Ln ['3' U1 Ordered Response Data Values 0'1 C) 53 C) 52 -1 o 1' Q Normal Quaniiles max (X) = 10.331 min (X) = 0.7993 Range = max (X) - min (X) = (10.331 - 0.7993) = 9.532 n _X? = X? +X3 + ... + X2 = 30.254 + 106.73 + ...+ 32.395 = 1654.09 i= 1 (n _MIX? ) -(EL, Xi)? (50 * 1654.09) - 72038.45 10665.94 n (n - 1) = 4.353 50 * 49 2450 (n In Ci-1 X?) - (EXi)' S = V4.353 = 2.086 n (n - 1) Lower Fence = Q1 - (1.5 * IQR) = 3.732 - (1.5 * 2.843) = 3.732 - 4.264 = -0.5322 Upper Fence = Q3 + (1.5 x IQR) = 6.575 + (1.5 * 2.843) = 6.575 + 4.264 = 10.839\fStatistic Value Mean 5.368 Median 5.656 Sample Size 50 Q1 3.732 Q3 6.575 Min 0.7993 Max 10.331 IQR 2.843 Range 9.532 Variance 4.353 Standard Deviation 2.086 Lower Fence -0.5322 Upper Fence 10.839