Question: An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 120 lb and 161 lb.

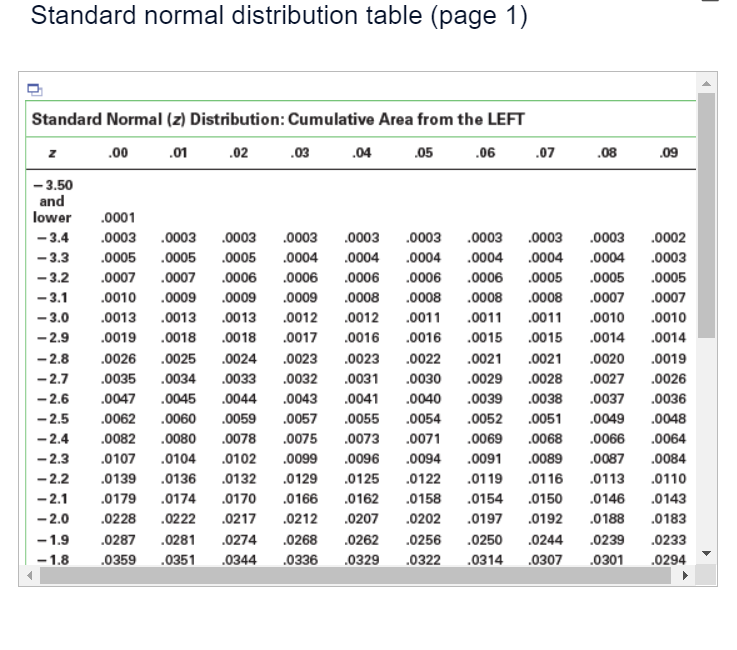
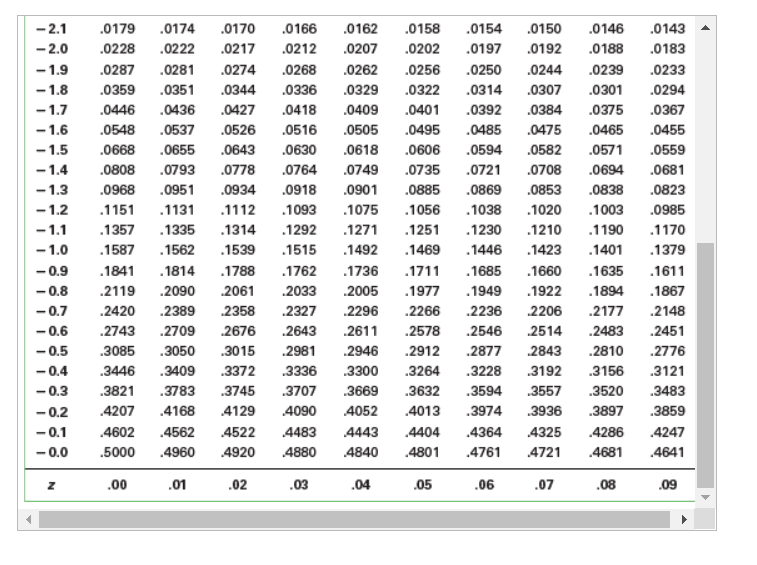
161 lb. The new population of pilots has normally distributed weights with

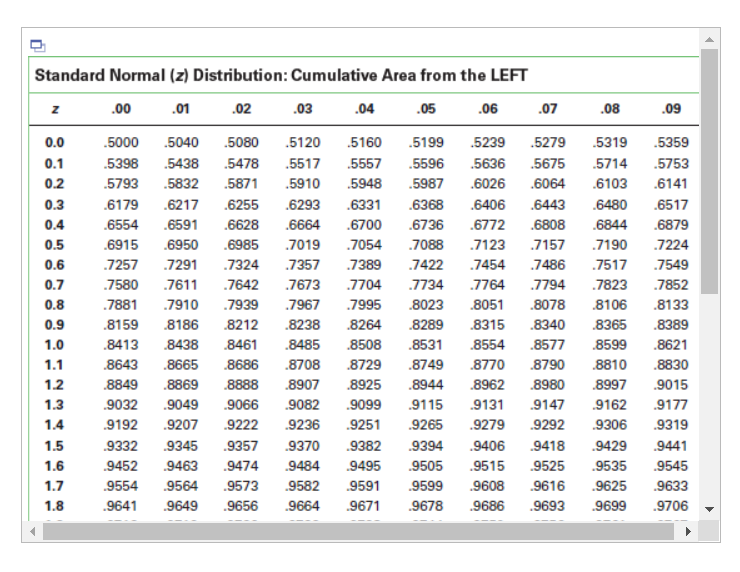
a mean of 127 lb and a standard deviation of 25.9 lb.

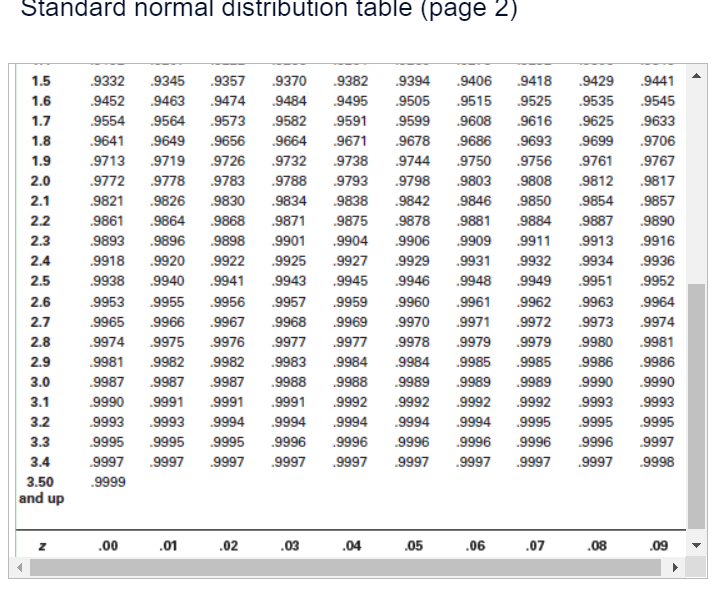
Click here to view page 1 of the standard normal distribution. Click

here to view page 2 of the standard normal distribution. a. If

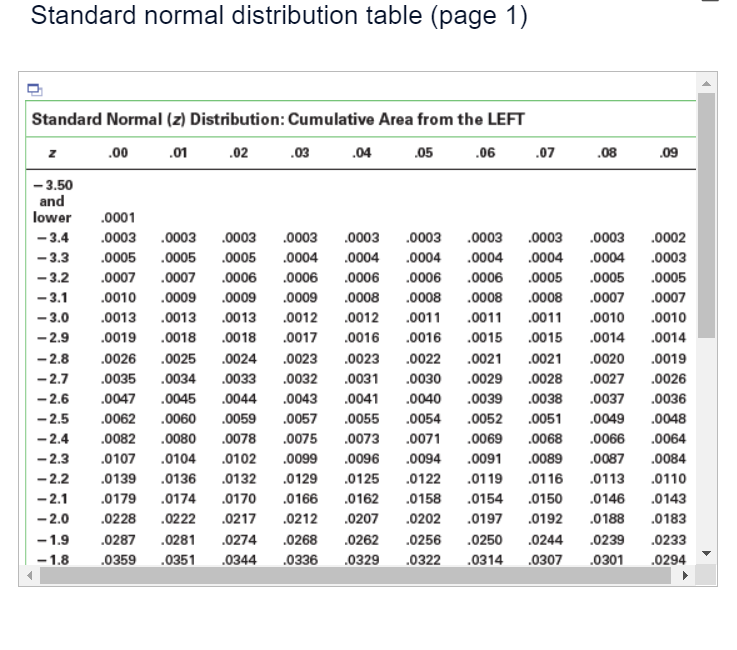
a pilot is randomly selected, find the probability that his weight is

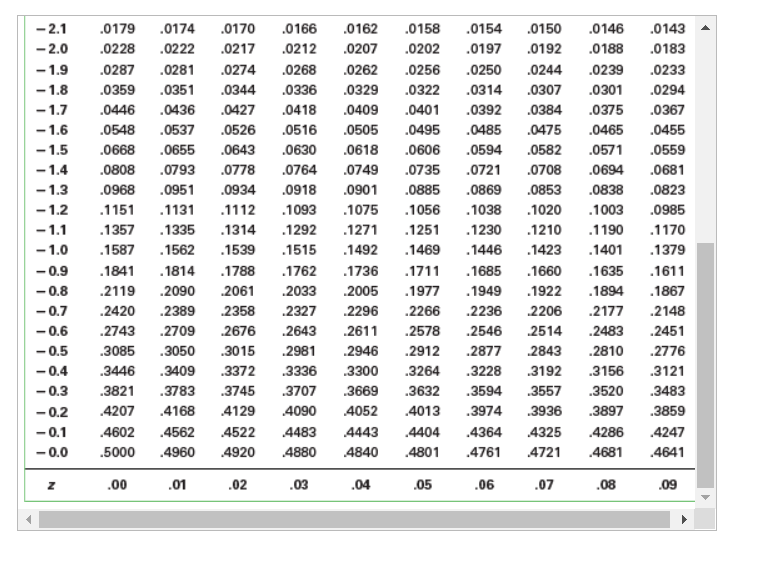
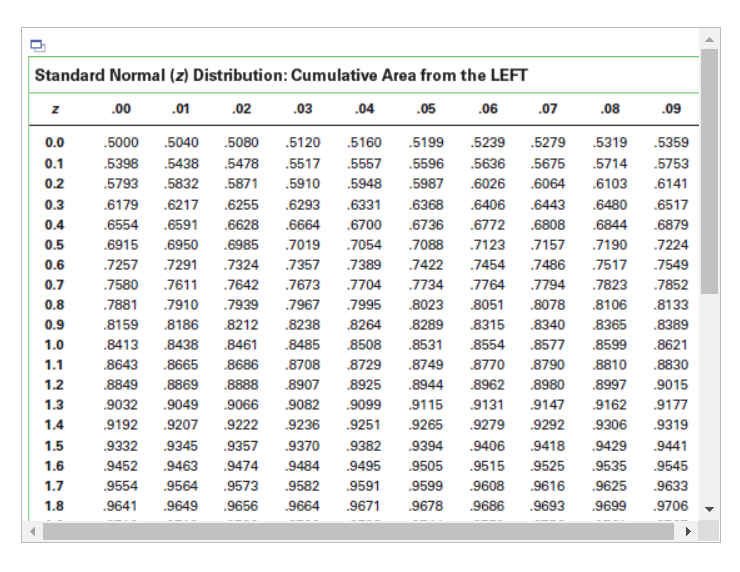
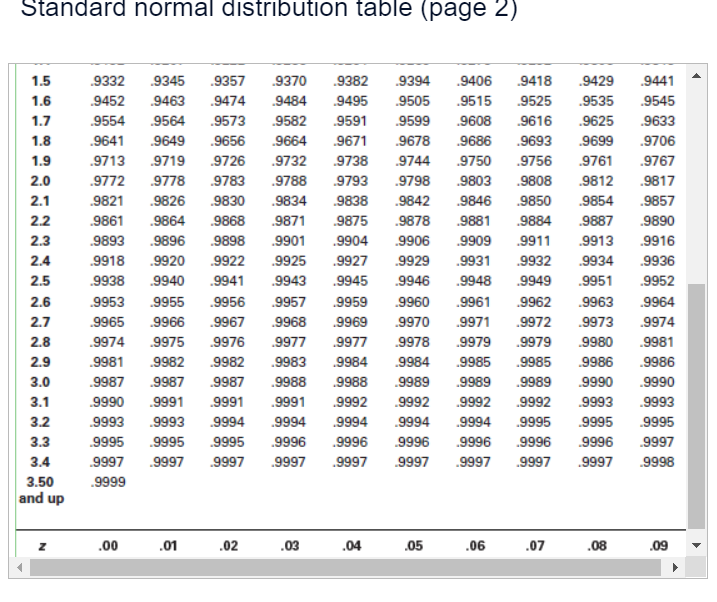
An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 120 lb and 161 lb. The new population of pilots has normally distributed weights with a mean of 127 lb and a standard deviation of 25.9 lb. Click here to view page 1 of the standard normal distribution. Click here to view page 2 of the standard normal distribution. a. If a pilot is randomly selected, find the probability that his weight is between 120 lb and 161 lb. The probability is approximately . (Round to four decimal places as needed.) b. If 30 different pilots are randomly selected, find the probability that their mean weight is between 120 lb and 161 lb. The probability is approximately . (Round to four decimal places as needed.) c. When redesigning the ejection seat, which probability is more relevant? O A. Part (a) because the seat performance for a single pilot is more important. O B. Part (b) because the seat performance for a sample of pilots is more important. O C. Part (a) because the seat performance for a sample of pilots is more important. O D. Part (b) because the seat performance for a single pilot is more important.Standard normal distribution table (page 1) Standard Normal (z) Distribution: Cumulative Area from the LEFT Z 00 .01 .02 .03 .04 .05 .06 .07 .08 .09 -3.50 and lower .0001 -3.4 .0003 0003 .0003 .0003 0003 .0003 .0003 .0003 0003 .0002 -3.3 .0005 .0005 .0005 .0004 .0004 .0004 .0004 .0004 .0004 .0003 -3.2 .0007 0007 .0006 .0006 .0006 .0006 0006 .0005 .0005 .0005 - 3.1 .0010 .0009 .0009 .0009 .0008 .0008 .0008 .0008 .0007 .0007 -3.0 .0013 0013 .0013 .0012 .0012 .0011 .0011 .0011 .0010 .0010 -2.9 .0019 0018 .0018 .0017 .0016 .0016 .0015 .0015 .0014 .0014 -2.8 .0026 .0025 .0024 .0023 .0023 .0022 .0021 .0021 0020 .0019 -2.7 .0035 0034 .0033 .0032 .0031 .0030 .0029 .0028 .0027 .0026 -2.6 .0047 0045 .0044 .0043 .0041 .0040 .0039 .0038 0037 .0036 -2.5 .0062 0060 .0059 .0057 .0055 .0054 .0052 .0051 .0049 .0048 -2.4 .0082 .0080 .0078 .0075 .0073 .0071 .0069 .0068 .0066 .0064 -2.3 .0107 0104 .0102 .0099 .0096 .0094 .0091 .0089 .0087 .0084 -2.2 .0139 .0136 .0132 .0129 .0125 .0122 .0119 .0116 .0113 .0110 -2.1 .0179 .0174 .0170 .0166 .0162 .0158 .0154 .0150 .0146 .0143 -2.0 .0228 .0222 .0217 .0212 .0207 .0202 .0197 .0192 .0188 .0183 - 1.9 .0287 .0281 .0274 .0268 .0262 .0256 .0250 .0244 .0239 .0233 - 1.8 .0359 .0351 .0344 .0336 0329 .0322 .0314 .0307 0301 .0294

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilot weighing between 129lb and 161 lb. the new population of pilots has normally distributed weights...

Stats question 1. ____________________________________ 2. (b) The probability for (b) above is (rounded to 4 places) 3.) ) (b) If 10 women are randomly selected, find the probability that they have a...

Submit quiz An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 120 lb and 181 lb. The new population of pilots has normally...

Exercise 1: An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 130 lb and 171 lb. The new population of pilots has normally...

This question: 18 point(s) possible Pro An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 130 lb and 171 lb. The new population of...

An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 140 lb and 191 lb. The new population of pilots has normally distributed weights...

An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 140 lb and 181 lb. The new population of pilots has normally distributed weights...

Zeroth, First, and Second Law of Thermodynamics illustration and result/reflection?

Explain exactly what is meant by the statement that "differentiation and integration are inverse processes."

Suppose there is a significant amount of money coming into the VC sector, with respect to historical trends. What does this imply about VC fund performance, and why?

construct an External Factor Evaluation (EFE) Matrix and Internal Factor Evaluation (IFE) Matrix for an automotive company.

3. If there are reasonable alternatives, think about your decisions based on the different reference points and see if there are any contradictions in the decisions.

4. It is only at this point that you can give the problem your full attention in relation to the various ways you have framed the problem.

1. To provide an insight into why a communication situation can be perceived differently depending on which psychological framework we choose to use.