An "expert" wrote something random and irrelevant right after I asked this a few min ago, so I wasted a question for this month. Please only respond with answers to the problem... thank you!!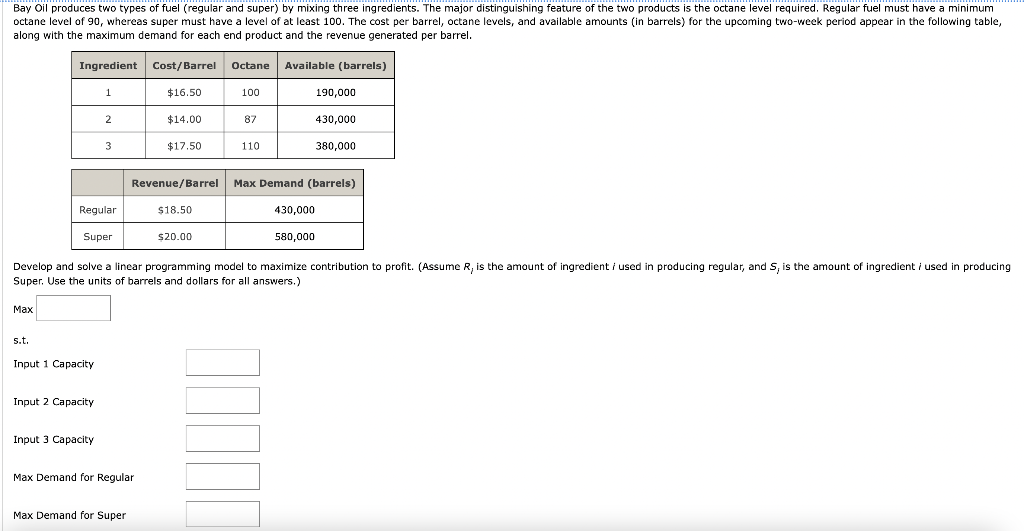

Bay oil produces two types of fuel (regular and super) by mixing three ingredients. The major distinguishing feature of the two products is the octane level required. Regular fuel must have a minimum octane level of 90, whereas super must have a level of at least 100. The cost per barrel, octane levels, and available amounts (in barrels) for the upcoming two-week period appear in the following table, along with the maximum demand for each end product and the revenue generated per barrel. Ingredient Cost/Barrel Octane Available (barrels) 1 $16.50 100 190,000 2. $14.00 87 430,000 3 $17.50 110 380,000 Revenue/Barrel Max Demand (barrels) Regular $18.50 430,000 Super $20.00 580,000 Develop and solve a linear programming model to maximize contribution to profit. (Assume R, is the amount of ingredient i used in producing regular, and S, is the amount of ingredient i used in producing Super. Use the units of barrels and dollars for all answers.) Max s.t. Input 1 Capacity Input 2 Capacity Input 3 Capacity Max Demand for Regular Max Demand for Super Max Demand for Super Required Octane Level, Regular Required Octane Level, Super R1, R2, R3, S1, S2, S3 2 0 ' What is the optimal contribution to profit? Report your values for R1, R2, R3, S1, S2, S3. (R1, R2, R3, 51, 52, 53) = ( What is the maximum profit (in dollars)? $