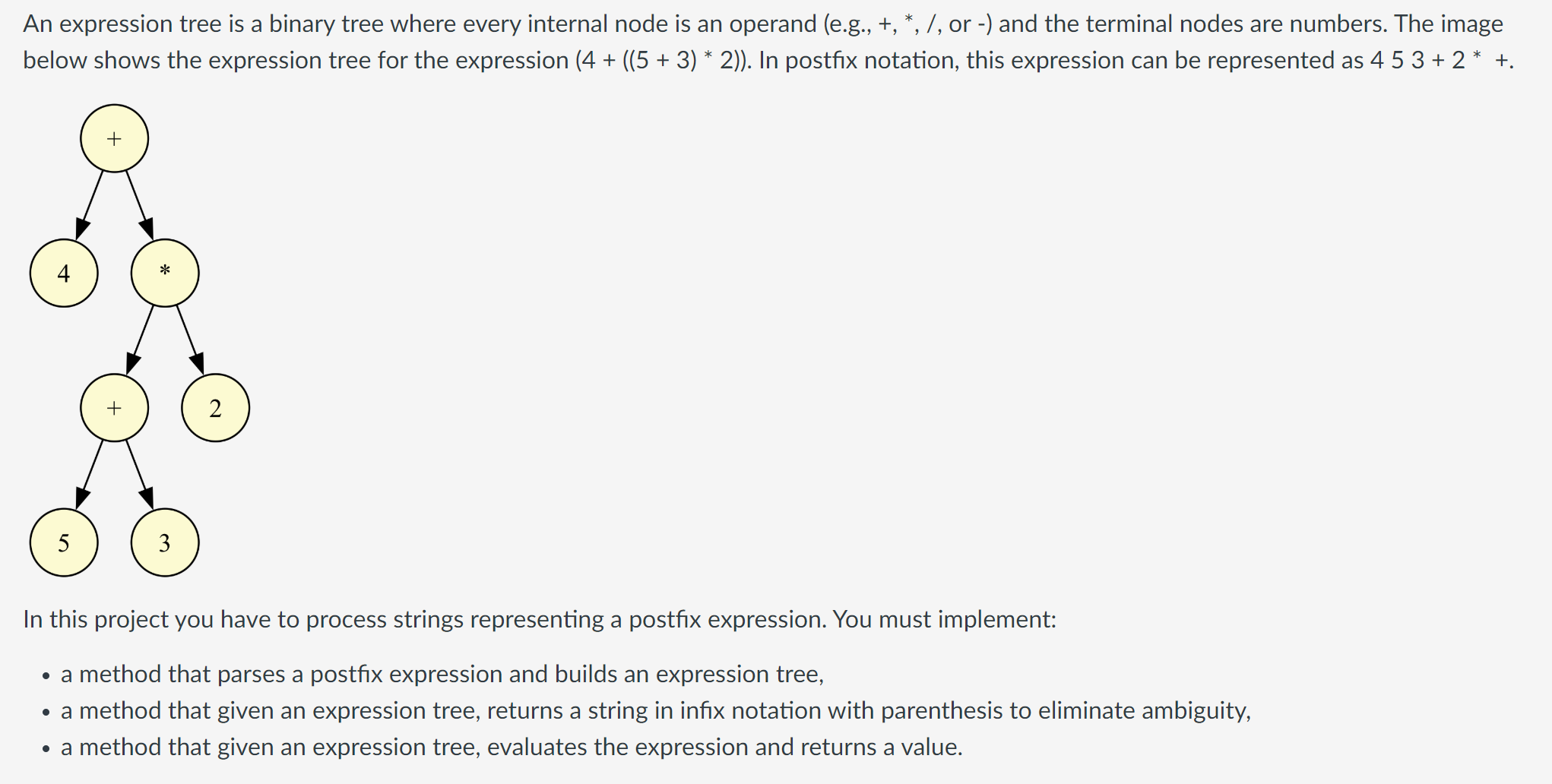
An expression tree is a binary tree where every internal node is an operand $($e$.$g$.,^(+),^(**),//,$ or $-)$ and the terminal nodes are numbers. The image

below shows the expression tree for the expression $(4+((5+3)**2)).$ In postfix notation, this expression can be represented as $453+2**+.$

In this project you have to process strings representing a postfix expression. You must implement:

a method that parses a postfix expression and builds an expression tree,

a method that given an expression tree, returns a string in infix notation with parenthesis to eliminate ambiguity,

a method that given an expression tree, evaluates the expression and returns a value.

ExpressionTree

Create a class called ExpressionTree that takes a string in postfix notation as an argument to the constructor. This class will store this expression and have methods that process the expression. The expression is readonly, can't be changed and the object of type ExpressionTree will represent that particular expression that is passed as argument to the constructor.

Define the following methods

ExpressionTree$($String postfix$)$

Constructor, stores the postfix expression in an instance variable for use in other methods of this class.

boolean parse$()$

Method that parses the postfix returning true if the expression is in valid postfix notation $($more on that below$).$ If the expression is valid, the routine, internally should build a BinaryNode tree and store the root in an instance variable.

BinaryNode getRoot$()$

Returns the root of the tree or null if either the tree hasn't been built yet $($i$.$e$.,$ parse$()$ has not been called$)$ or if parse$()$ returns false negative and thus there is no tree.

int evaluate$()$ throws ArithmeticExpression

Method evaluates the tree stored internally and returns an integer representing the value of the expression. The expression should support addition $(+),$ multiplication $(*),$ subtraction $(-)$ and division$(/).$ Note that division requires two special cases. First, check that you don't do division by $0$ and second, make sure that the division is done using integer division $($casting values$)$ so that the result is always inter. This expression evaluator is a an integer expression evaluator. What to do when you divide by $0?$ Do the same that Java does, thrown an exception $($ArithmeticException$).$ You must declare this method to thrown this exception.

String infixNotation$()$

Return an infix notation with parenthesis to enforce order of operations. The terminal nodes of the tree contain values $($i$.$e$.,$ number$)$ and thus should not be wrapped in parenthesis. But all other subtrees should be turned into a parenthesized expression. This is in effect an in$-$order traversal of the tree.

Algorithm to parse postfix

The algorithm to parse a postfix expression is the same as we saw in class earlier in the semester. It uses a stack to store values as it is processing the postfix expression. In this project, stack will store BinaryNode objects. Thus you need a local variable in the parse$()$ method of type Stack$>.$ We will look for this in the code as part of the $20$ points for Design. Please note that this algorithm was discussed in the WATCH video on Stacks during Module $2/$Week $7.$

while more tokens if $($token is a number$)$ build a BinaryNode with number as value $($left and right are null$)$ push node leaf in Stack else if token is operator

$//$ and there are $2$ values in the stack right pop the stack left pop the stack build a new BinaryNode with operator as root and left, right subtrees push new BinaryNode back onto the stack

else

$//$ this is an error, return false

Test$-$driven development dictates that you should do some testing, then some development, then some testing again, and repeat until all of your code is written and it passes all of your tests. Write test cases for this class that verifies that all the methods work as expected. Your test cases should be stored in a file called ExpressionTreeTest and call all methods in the class. The test cases should execute every line of the code in ExpressionTree$$for you to get $100\%$ on testing and coverage.

We strongly recommend you build the test cases first, following the idea of test driven development. Build a list of expressions and know ahead of time what those expressions would evaluate to and how they would be represented in infix notation. Use those examples to build the test cases and run them until all of your code gets $100\%$ functional results $($all test cases pass$)$ and you get $100\%$ coverage $($all of your lines are executed$).$

The table below shows some cases that you should consider as you understand this project specification. What other cases would you add? Add a few more examples that cover additional cases. For example, have one expression that divides by $0.$ Write JUnit test cases based on these expressions.

PostfixInfixEvaluation$34+(3+4)734*5+((3*4)+5)17345*+(3+(4*5))2310101023+45*+5/(((2+3)+(4*5))/5)5$ Test$-$driven development dictates that you should