Question: An integral transform is defined as F ( w ) = 0 L f ( x ) s i n ( n L x )
An integral transform is defined as
where dots and is a constant for the domain. Apply the integration by parts to prove that this transform to ie requires two boundary conditions: at and at with A and being constants. Explain whether this transform can be used to solve the ordinary differential equation with at and at points
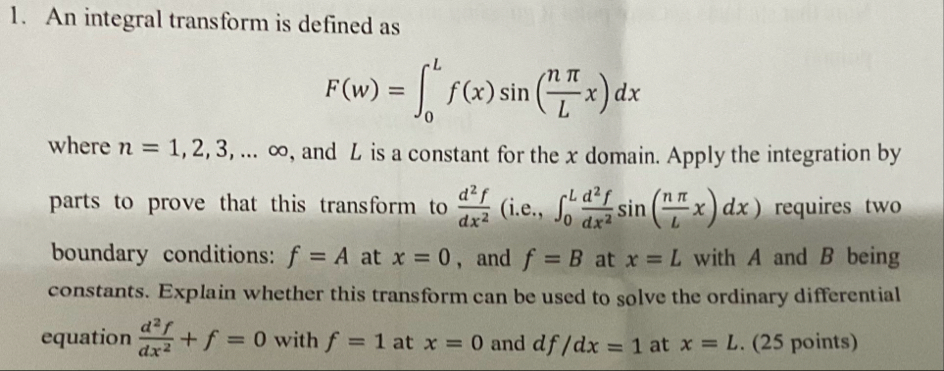
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


