Question: ...................... An island is n island is .13 mi due north of its closest point along a straight shoreline. Aguard is staying at a cabin

n island is .13 mi due north of its closest point along

......................

An island is

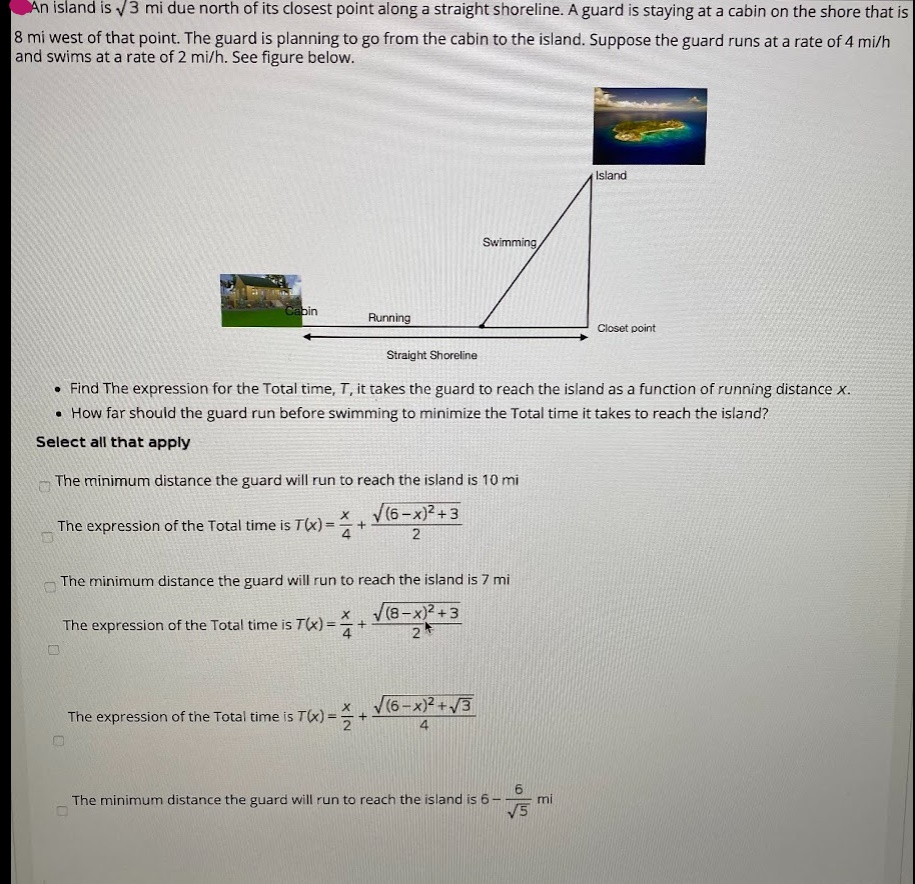
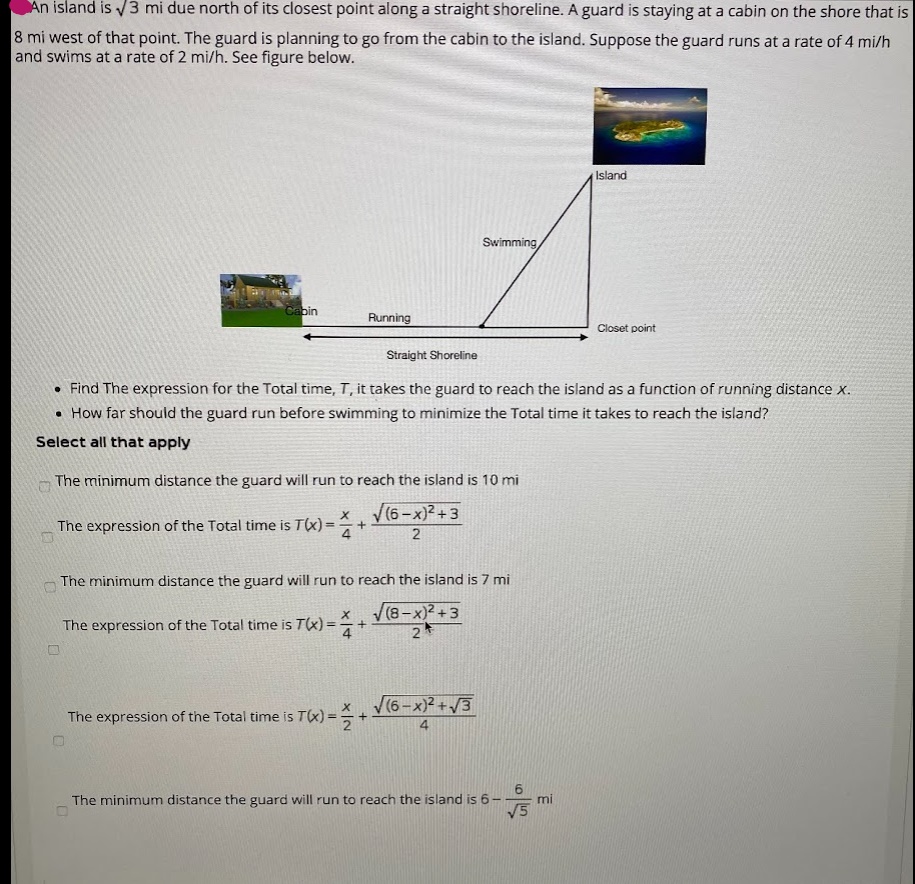
n island is .13 mi due north of its closest point along a straight shoreline. Aguard is staying at a cabin on the shore that is 8 mi west of that point. The guard is planning to go from the cabin to the island. Suppose the guard runs at a rate of 4 mi/h and swims at a rate of 2 mi/h. See figure below. Stra&ht Find The expression for the Total time, T, it takes the guard to reach the island as a function of running distance X. How far should the guard run before swimming to minimize the Total time it takes to reach the island? Select all that apply The minimum distance the guard will run to reach the island is 10 mi The expression of the Total time is T CK) + 2 The minimum distance the guard will run to reach the island is 7 mi The expression of the Total time is T (X) The expression of the Total time ts T(x) x 4 6 The minimum distance the guard will run to reach the island is 6

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

I have posted example 4.34 below, but I need help with part 2. Part 1 is given for context. Part I: Complete the following steps: 1. Read Example 4.34 in Section 4.7 of Calculus, Volume 1. 2....

An island is 22 mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is 66 mi west of that point. The visitor is planning to go from the...

I need help with these questions 8. Sketch a graph of f(x) = (x - 1)3 (x + 2) labeling everything on the side. 9. Sketch a graph of f(x) = _ labeling as much as possible on the side. heaw...

I need help with part 2, part 1 is there for context. Question: Part I An island is 2mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is...

Applied Optimization An island is 2 . 3 m i due north of its closest point on a straight shoreline. A visitor is staying at a cabin on the shore that is 6 . 4 m i from that point. The visitor is...

An island is2midue north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is6miwest of that point. The visitor is planning to go from the cabin to...

4. Using the financial ratios provided by eVal, evaluate any trends in Royal Caribbean?s return on equity, compare it with Carnival Cruise?s return on equity, and discuss the main causes of any...

Chapter 1 Location \"Location, Location, Location!\" Chapter Objectives On completion of this chapter the reader will understand: The influence that location has on occupancy The relationship between...

For the exclusive use of A. Bennis, 2015. MH0005 0 0 7 7645065 Fra nk T. R othaermel M ichael Jano vec InterfaceRAISE (in 2010): Raising the Bar in Sustainability Consulting MR. JIM HARTZFELD walked...

Suppose h is continuous on [0, 10] and h(0) = h(10). Prove that there exists x, y [0, 10] such that ly - x = 5 and h(x) = h(y).

In a period of 100 minutes there were a total of 190 arrivals at a highway toll booth. The accompanying table shows the frequency of arrivals per minute over this period. Test the null hypothesis...

2 How is the source of heat shown in Figure 10.1 different from the laboratory heat sources we use today?

The Central Biloxi Motel located in the state of Mississippi has 216 rooms available to guests. The motel is readily accessible to interstate highways 75 and 85 and to state highways 23 and 41. The...

3. Try to clarify how you think when you are going to write a note aimed at influencing the leader of the department. Remember, it is not what you think, but how you think that should be clarified....

2. Take as your starting point a conflict you experienced recently with a close friend. Try to go through the communication that took place and answer the following questions: a) What was the main...

2. In this chapter, the reader should reflect on the following concepts: Differences, relationships, processes, patterns, contexts, symmetrical rela-tionships, complementary relationships, linear...