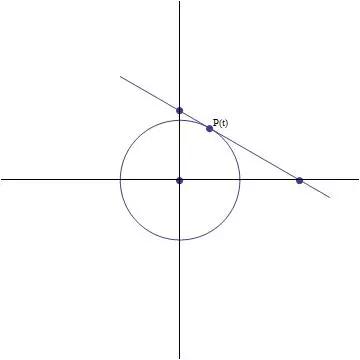
Question: An object is moving around the unit circle with parametric equations x(t)=cos(t), y(t)=sin(t) , so it's location at time t is P(t)=(cos(t),sin(t)) . Assume 0
An object is moving around the unit circle with parametric equations x(t)=cos(t), y(t)=sin(t), so it's location at time t is P(t)=(cos(t),sin(t)) . Assume 0 < t < π/2. At a given time t, the tangent line to the unit circle at the position P(t) will determine a right triangle in the first quadrant. (Connect the origin with the y-intercept and x-intercept of the tangent line.)
(a) The area of the right triangle is a(t)= .
(b) lim t → pi/2−a(t)=
(c) lim t → 0+a(t)=
(d) lim t → pi/4 a(t)=
(e) With our restriction on t, the smallest t so that a(t)=2 is
(f) With our restriction on t, the largest t so that a(t)=2 is
(g) The average rate of change of the area of the triangle on the time interval [π/6,π/4] is .
(g) The average rate of change of the area of the triangle on the time interval [π/4,π/3] is .
(h) Create a table of values to study the average rate of change of the area of the triangle on the time intervals [π/6,b], as b approaches π/6 from the right. The limiting value is .
(i) Create a table of values to study the average rate of change of the area of the triangle on the time intervals [a,π/3], as a approaches π/3 from the left. The limiting value is .
P(t)
Step by Step Solution
3.43 Rating (143 Votes )
There are 3 Steps involved in it
we knao Jhat area of tmogk tormula alt 2 fnt olt Sin2t le Smallest t so Ahat at 2 is ... View full answer

Get step-by-step solutions from verified subject matter experts