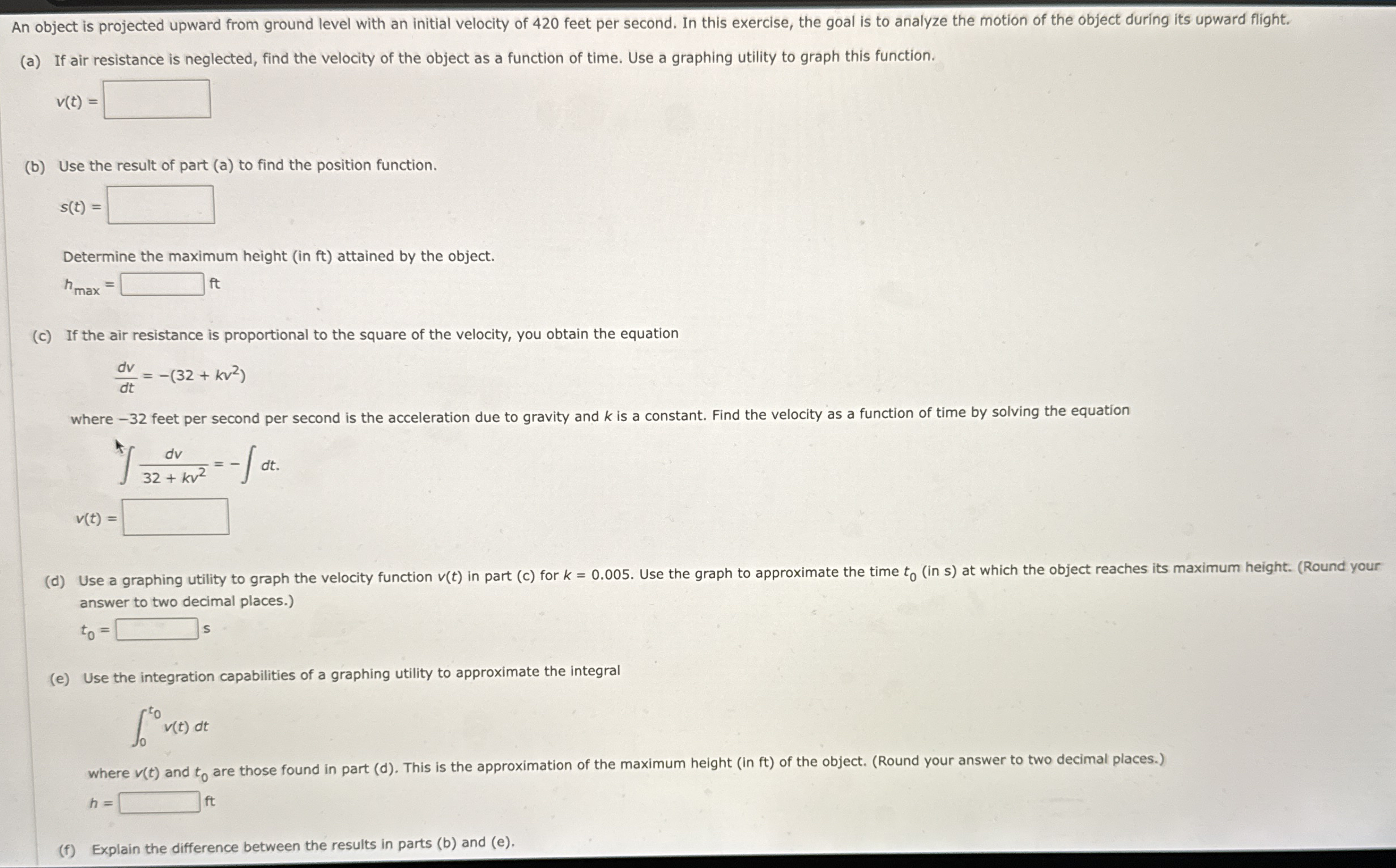
An object is projected upward from ground level with an initial velocity of $420$ feet per second. In this exercise, the goal is to analyze the motion of the object during its upward flight.

$($a$)$ If air resistance is neglected, find the velocity of the object as a function of time. Use a graphing utility to graph this function.

$v(t)=$

$($b$)$ Use the result of part $($a$)$ to find the position function.

$s(t)=$

Determine the maximum height $($in ft $)$ attained by the object.

$h_{\text{m}\text{a}\text{x}}=$

$$ ft

$($c$)$ If the air resistance is proportional to the square of the velocity, you obtain the equation

$\frac{dv}{dt}=-(32+k{v}^2)$

where $-32$ feet per second per second is the acceleration due to gravity and $k$ is a constant. Find the velocity as a function of time by solving the equation

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{dv}{32+k{v}^2}=-{\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}dt.$

$v(t)=$

$($d$)$ Use a graphing utility to graph the velocity function $v(t)$ in part $($c$)$ for $k=0\mathrm{.}005.$ Use the graph to approximate the time $t_0($in $s)$ at which the object reaches its maximum height. $($Round your answer to two decimal places.$)$

$t_0=,s$

$($e$)$ Use the integration capabilities of a graphing utility to approximate the integral

${\displaystyle \underset{0}{\overset{t_0}{}}}v(t)dt$

where $v(t)$ and $t_0$ are those found in part $($ d $).$ This is the approximation of the maximum height $($in ft $)$ of the object. $($Round your answer to two decimal places.$)$

$h=$ ft

$($f$)$ Explain the difference between the results in parts $($b$)$ and $($e$).$