An unknown linear programing cost minimization problem has been solved. There were three products involved, X1, X2, and X3. The answer and sensitivity reports are attached here. Answer the questions that follow. Note, critical information has been purposefully removed so you wont be able to reproduce the result on a computer. You will have to rely only on your understanding of the computer report to answer the questions.

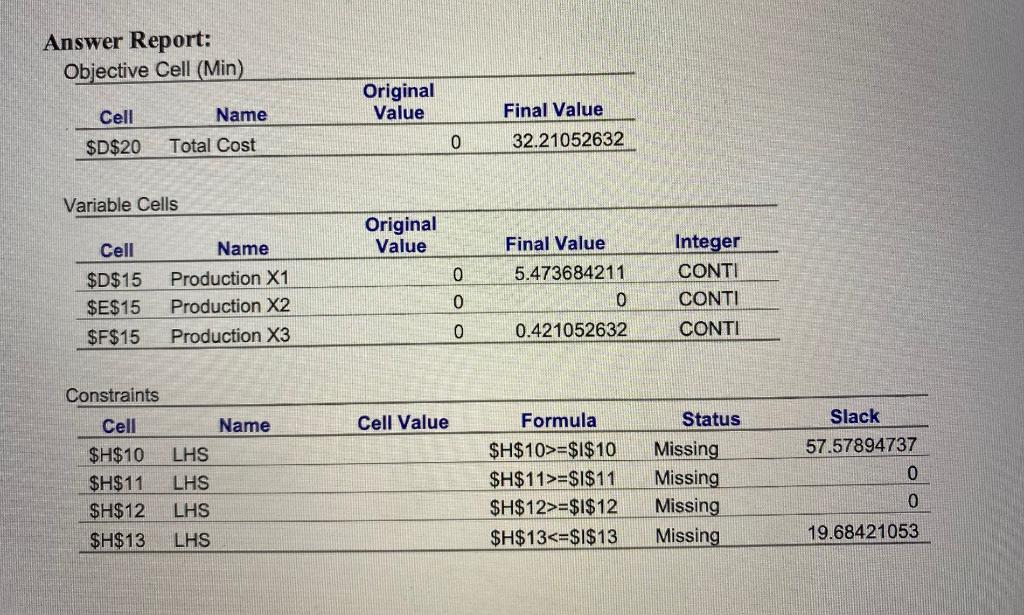
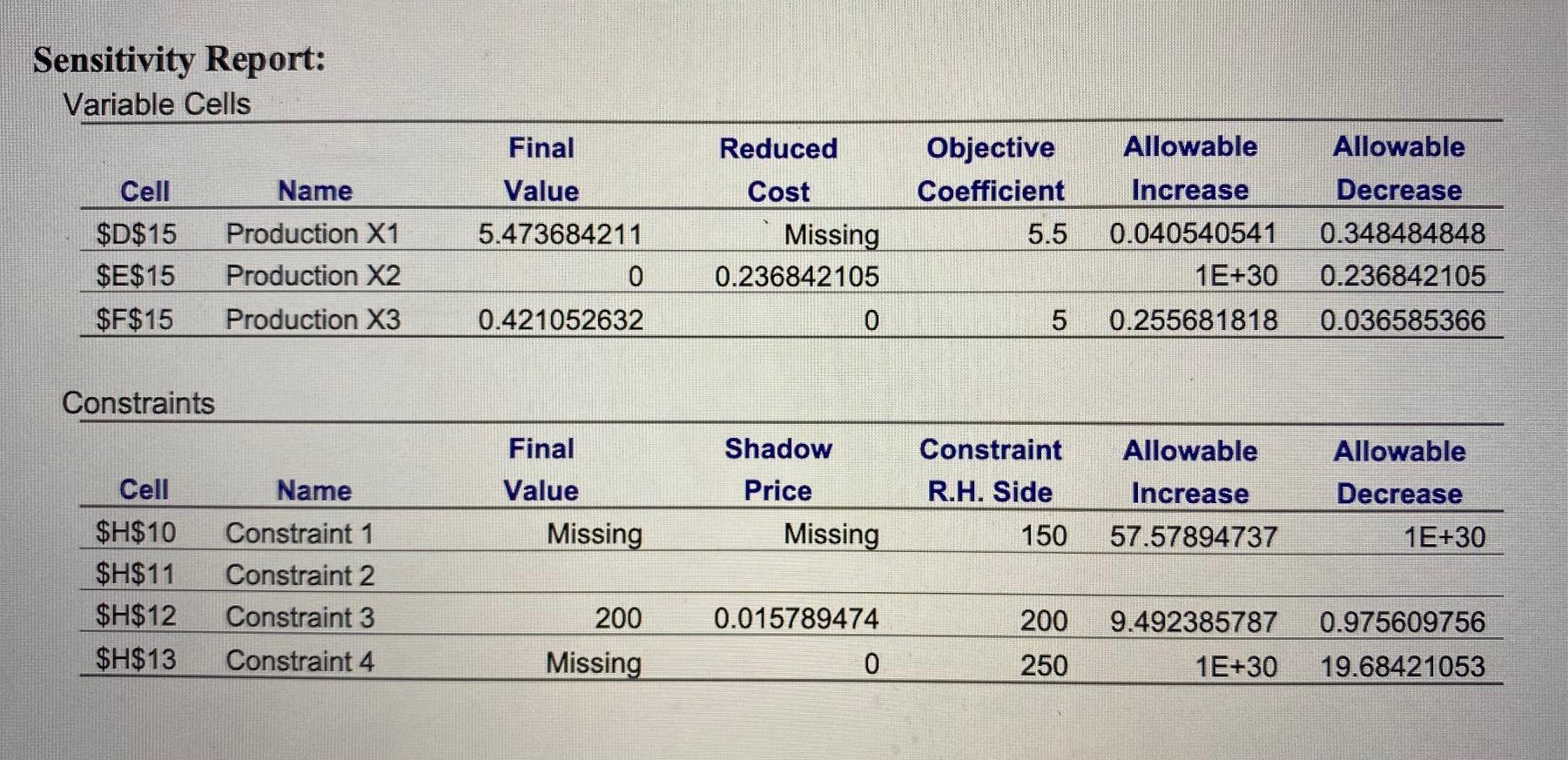
1. Find out what is the minimized total cost and how much the three products should be produced.

2. In the answer report, replace the four cells under Status that are marked by missing by either binding or not binding. State the reason why you believe so

3. In the sensitivity report, replace the missing cell in Reduced Cost by an actual number and state why you chose that value

Answer Report: Objective Cell (Min) Original Value Cell Final Value Name Total Cost $D$20 0 32.21052632 Variable Cells Original Value Cell 0 $D$15 $E$15 $F$15 Name Production X1 Production X2 Production X3 Final Value 5.473684211 0 0.421052632 Integer CONTI CONTI CONTI 0 0 Constraints Cell Value Status Cell $H$10 $H$11 $H$12 $H$13 Name LHS LHS LHS Formula $H$10>=$1$10 $H$11>=$1$11 $H$12>=$1$12 $H$13