Answe number 1

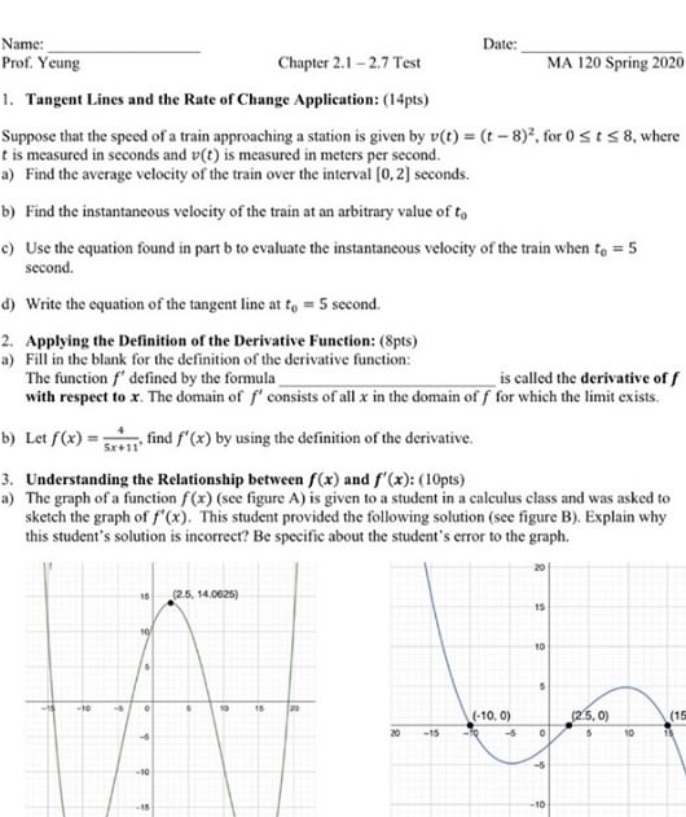
Name: Date: Prof. Yeung Chapter 2.1 - 2.7 Test MA 120 Spring 2020 1. Tangent Lines and the Rate of Change Application: (14pts) Suppose that the speed of a train approaching a station is given by v(t) = (t -8) , for 0 S t S 8, where t is measured in seconds and v(t) is measured in meters per second. a) Find the average velocity of the train over the interval [0, 2] seconds. b) Find the instantaneous velocity of the train at an arbitrary value of to c) Use the equation found in part b to evaluate the instantaneous velocity of the train when to = 5 second. d) Write the equation of the tangent line at to = 5 second. Applying the Definition of the Derivative Function: (8pts) Fill in the blank for the definition of the derivative function: The function f' defined by the formula is called the derivative of f with respect to x. The domain of f' consists of all x in the domain of f for which the limit exists. b) Let f (x) = . find f'(x) by using the definition of the derivative. 3. Understanding the Relationship between f(x) and f'(x): (10pts) The graph of a function f(x) (see figure A) is given to a student in a calculus class and was asked to sketch the graph of f'(x). This student provided the following solution (see figure B). Explain why this student's solution is incorrect? Be specific about the student's error to the graph. (25, 14.0625) (-10, 0) (25, 0) (15 -15