answer all parts clear

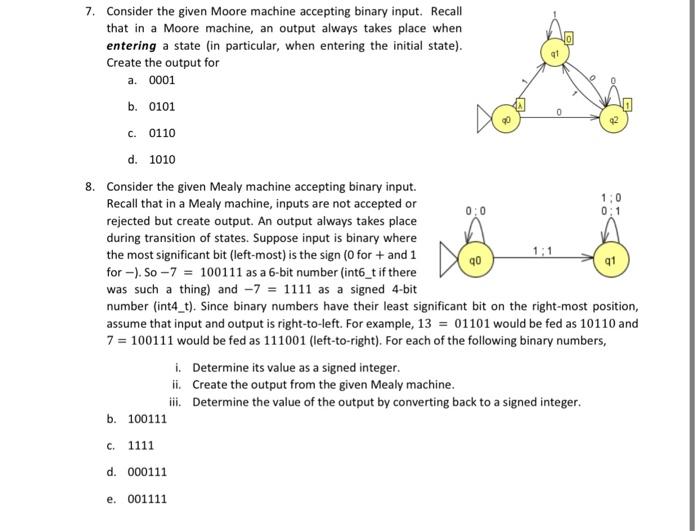
7. Consider the given Moore machine accepting binary input. Recall that in a Moore machine, an output always takes place when entering a state (in particular, when entering the initial state). Create the output for a. 0001 b. 0101 c. 0110 d. 1010 8. Consider the given Mealy machine accepting binary input. Recall that in a Mealy machine, inputs are not accepted or rejected but create output. An output always takes place during transition of states. Suppose input is binary where the most significant bit (left-most) is the sign ( 0 for + and 1 for - ). So 7=100111 as a 6 -bit number (int6_t if there was such a thing) and 7=1111 as a signed 4 -bit number (int4_t). Since binary numbers have their least significant bit on the right-most position, assume that input and output is right-to-left. For example, 13=01101 would be fed as 10110 and 7=100111 would be fed as 111001 (left-to-right). For each of the following binary numbers, i. Determine its value as a signed integer. ii. Create the output from the given Mealy machine. iii. Determine the value of the output by converting back to a signed integer. b. 100111 c. 1111 d. 000111 e. 001111