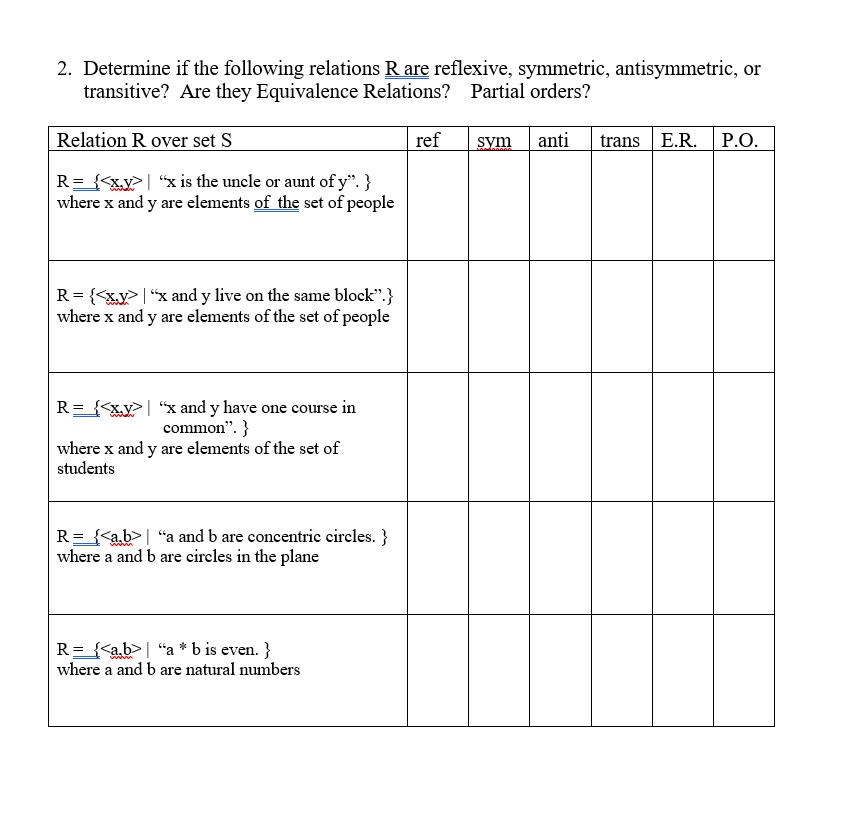
Answer all questions fully (no discontinuous fragments), in sequential order. Explain all answers: show all computations, proofs, analyses. decisions, steps, and programs. Best of prospects. 1. A. If S is the set of people and the relation R over set S is: 733$ 5ft '5; and y have the same integer shoe size (inches only. no fractions)\". Determine if the relation R is: reexive , symmetric , antisymmetric , transitive , equivalence relation , partial order , B. Fill in which properties the following relations on {1, 2, 3, 4} satisfy? R = {(1, 3'), (1, 2), (2, 2), (3, 2'), (4.11), (2, 1LL TraSitivei Symmetric: R: {(1, 1), (2, 2), (2, 1), (3, 3'),(1.. 2), (4:3)} TfaSitivei Symmetric: R: {(1. 1), (2. 2), (2, 1), (1.. 2M3, 4), (4,3)} Transitive: Symmetric: Antisymmetric: R= {(1, l), (4, 4), (1, 2), (2, 3'), (1, 3) } Transitive: Anti symmetric: 2. Determine if the following relations R are reflexive, symmetric, antisymmetric, or transitive? Are they Equivalence Relations? Partial orders? Relation R over set S ref sym anti trans E.R. P.O. R= { xy> | "x is the uncle or aunt of y". } where x and y are elements of the set of people R = {| "x and y live on the same block".} where x and y are elements of the set of people R= { xy>| "x and y have one course in common". } where x and y are elements of the set of students R= { ab>| "a and b are concentric circles. } where a and b are circles in the plane R= {ab>| "a * bis even. } where a and b are natural numbers3. A. If S is the powerset: { {). (1). (2): (3): (1.2), (2,3). (1,3), (1,2,3) and the relation R is: xRy iff "x is a subset of y" written X By. Draw the Hasse diagram below: 3.B. What is the most visible and important application area of relations to Computer Science? 3.C The set S = {1, 2, 3, 4, 5, 6 ) has a relation R specified by its matrix (below) So xRx iff "there is a 1 in the cell at row x (counting from the top as 1) and column y (counting from the leftmost as column 1)". Is the relation R reflexive symmetric antisymmetric or transitive ? (4 questions) 1 2 I+ 6 0 0 1 0 1 0 0 Oth 0 0 0 0 0 0 0 0 0 0 4. A. Consider the set S = { 1, 2, 3 , 6. 8, 9, 27, 32 }. A relation R is defined over S such that xRy if "x divides into y". Draw the Hasse diagram. Make sure the minimal element is at the bottom and the maximal ones at the top. B. Look at the relation x Ry iff y % 6=x %6 over Natural Numbers . The % is the remainder operator, also called mod. Determine (write down) the Equivalence Classes (partitions) which this equivalence relation formed. List the equivalence classes below (giving 3 members of each partition)