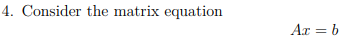
Answer all the questions in details, please!

2. This problem has two parts. (a) Before paying employee bonuses, state and federal taxes, a company earns a profit of $60,000. The company pays employees a bonus equal to 5% of after-tax profits. State tax is 5% of profits (after bonuses are paid). Finally federal tax is 40% of profits (after bonuses and state tax are paid). Write a system of linear equations to find the amounts paid in bonuses, state tax and federal tax. (b) Show that the set of solutions of the linear equation a1x1++anxn=b is a convex set. 3. Consider the matrix A=213434151011011211230224 Use Gaussian elimination to answer (a) to (c) below. (a) Find a basis for the row space of A. Explain your answer. (b) Find a basis for the column space of A. Explain your answer. (c) Find a basis for the null space of A. Explain your answer. (d) What are dim(N(A)), dim(R(A)) and dim(C(A)) ? (e) Find a vector in N(A) and a vector in R(A) and show that the vectors are orthogonal. 4. Consider the matrix equation Ax=b where A=[A1A2A3A4A5] is a 35 matrix with columns A1,,A5 and b is a 31 column vector. Let x=34307 be a solution of the above matrix equation. (a) Express b in terms of the columns of A. (b) Consider the augmented matrix A=[Ab]. Determine if the equation has a solution in the following cases. Justify your answer in each case. i. rank(A)=3 and rank(A)=3. ii. rank(A)=2 and rank(A)=3. iii. rank(A)=1 and rank(A)=2. iv. rank(A)=1 and rank(A)=3. Is this possible? (c) Using your answers to the previous question state how you can determine if Ax=b has a solution by just knowing the ranks of the matrices A and A. (d) If M is a 33 matrix show that M[Ab]=[MAMb]. Next we'll focus on the rows of A and write A as A=R1R2R3 where R1,R2 and R3 are the rows of A (each Ri is itself a 5-dimensional vector). Let R be an arbitrary vector in the row space of A. (e) Is {R,R1,R2,R3} a linearly independent set of vectors? (f) Show that every vector in the null space is orthogonal to every vector in the row space. (g) What is the dimension of the null space of an invertible square matrix M ? 5. Let A be an mn matrix (m<>