Answer all these math questions and show your work and explain.

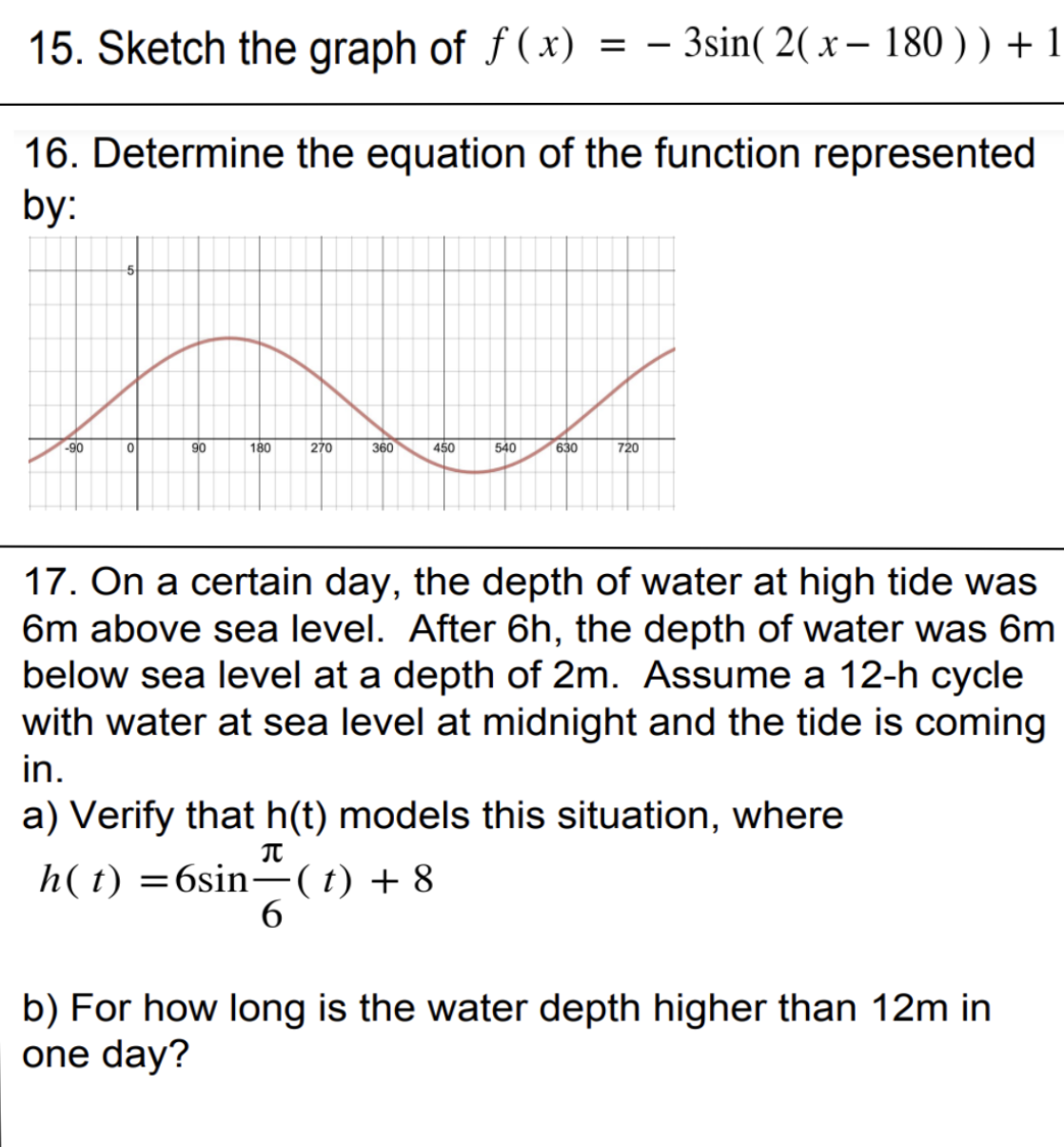
15. Sketch the graph of f(x) = 3sin(2(x-180)) + 1 16. Determine the equation of the function represented 17. On a certain day, the depth of water at high tide was 6m above sea level. After 6h, the depth of water was 6m below sea level at a depth of 2m. Assume a 12-h cycle with water at sea level at midnight and the tide is coming in. a) Verify that h(t) models this situation, where h(t) =6sin%( ) + 8 b) For how long is the water depth higher than 12m in one day? Question 17 This question involves verifying and working with the function h[t} = 6 sin (%t) L that models the tidal heights over time. Part a: Verify h(t) To vernify that h-l:_t} models the situation, we need to plug in the given values into the function and see if they match the scenario described. 1. At high tide (which we can assume is at = (0 for midnight), the depth of water was 6m above sea level, so h.[} should equal 14m (8m sea level + 6m high tide). 2. After 6 hours, the depth of water was 6m below sea level, so it [6] should equal 2m (8m sea level - 6m low tide). Part b: Duration of Water Depth Above 12m We want to find the time periods during which the water depth is greater than 12m. This means solving the inequality hft} > 12 within one cycle, which is 12 hours. Part a: Verification of h(t) .. Att = 0 (midnight), the depth of water is h(0) = 8 meters. This does not match the expected 14 meters. This suggests that our assumption about high tide being at midnight might not be correct, or that there is a different starting point for . 2. After 6 hours ( = 6), the depth of water is also h(6) = 8 meters. This does not match the expected 2 meters, indicating again that our assumptions may need to be adjusted, or the function does not perfectly model the situation as described. Part b: Duration of Water Depth Above 12m The solution to the inequality h.{_t) > 12 yields two sets, represented in a general form 2\"55 and multiples of 7, which will give us the exact points involving the arctangent of in time when the tide is at 12 meters. These points are given in intervals of 6 multiplied by the solutions to the equation h(t} = 12, which are derived from the intersection of the sine function with the line at h(t) = 12. The calculations reveal the following: Part b: Duration of Water Depth Above 12m * The water starts to rise above 12 meters at approximately = 1.39 hours. * The water falls below 12 meters again at approximately = 4.61 hours. These times represent the interval within the first 12-hour cycle where the water depth is higher than 12 meters. However, the order of the times seems counterintuitive, as we'd expect the starting time to be smaller than the ending time. This likely indicates that the start time is actually when the tide is coming down from its peak, and the end time is when it's rising, given the nature of the sine wave and the tidal patterns. To find out for how long the water is above 12m, we need to subtract the end time from the start time and take the absolute value to ensure a positive duration