Question: Answer as fast as possible please: 1. .-'-'-. population is modeled by the differential equation = 1.5P[1 i) sit 44 DC] {a} For I.yhat values
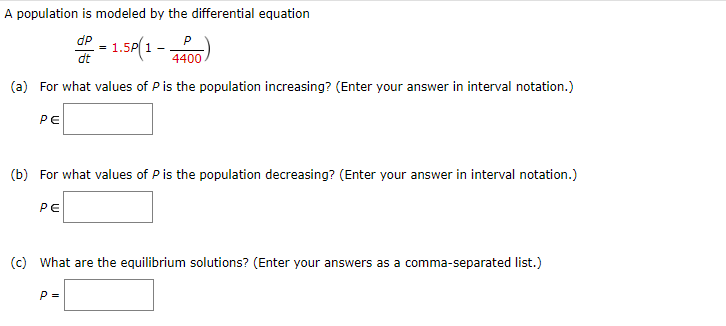
![the differential equation = 1.5P[1 i) sit 44 DC] {a} For I.yhat](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661437e1c29b_3026661437e079a5.jpg)
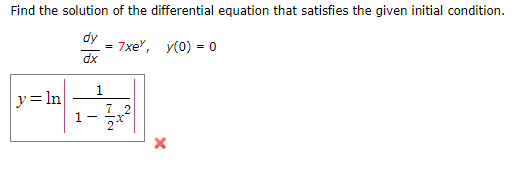
Answer as fast as possible please:
1.
![notation.) P 6S {o] For I.yhat values of P is the population](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661437ea820f_3026661437e91df0.jpg)
![decreasing? [Enter your answer in interyal notation.] P 6S {(3 1.that are](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661437eee9f4_3026661437ee1449.jpg)
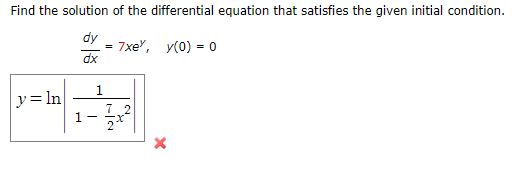
.-'-'-. population is modeled by the differential equation = 1.5P[1 i) sit 44 DC] {a} For I.yhat values of P is the population increasing? {Enter your answer in interval notation.) P 6S {o] For I.yhat values of P is the population decreasing? [Enter your answer in interyal notation.] P 6S {(3 1.that are the equilibrium solutions? (Enter your answers as a commaseparated list.) Find the solution of the differential equation that satisfies the given initial condition. dy = 7xey, V(0) = 0 dx 1 y = In 1 - X X
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


