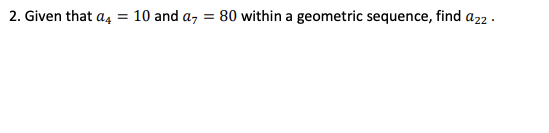
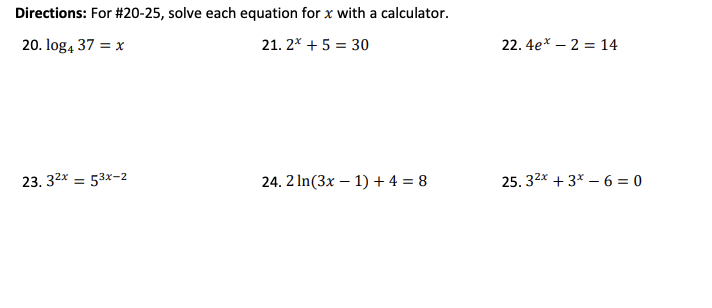
Answer each question from the pictures given below regaurding Logs, Exponential Functions, and Sequences. Make sure to show all work and steps to each answer! Circle your final answer for each question.

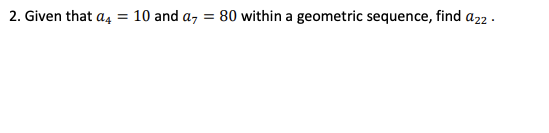
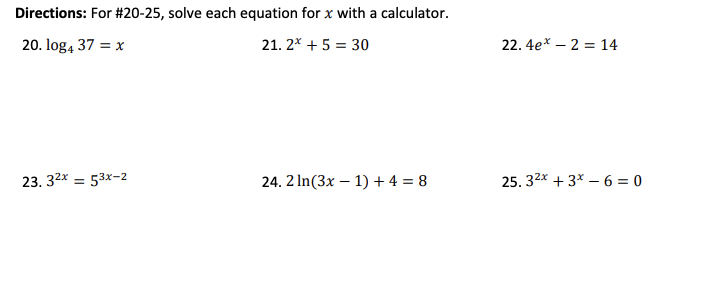
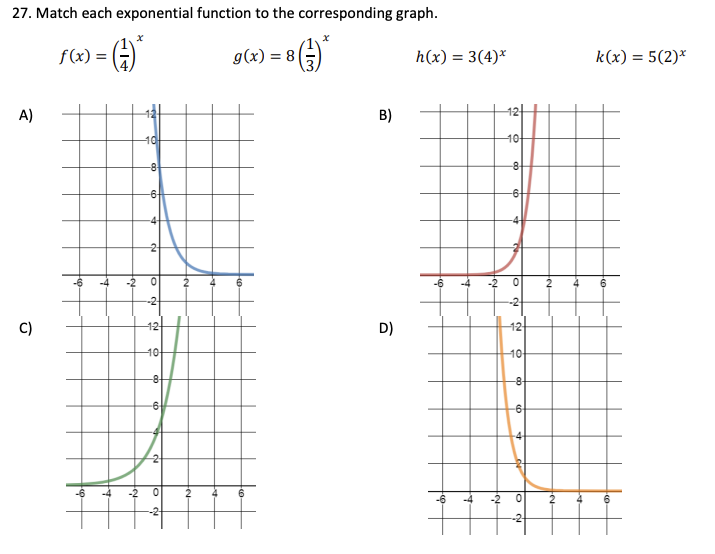
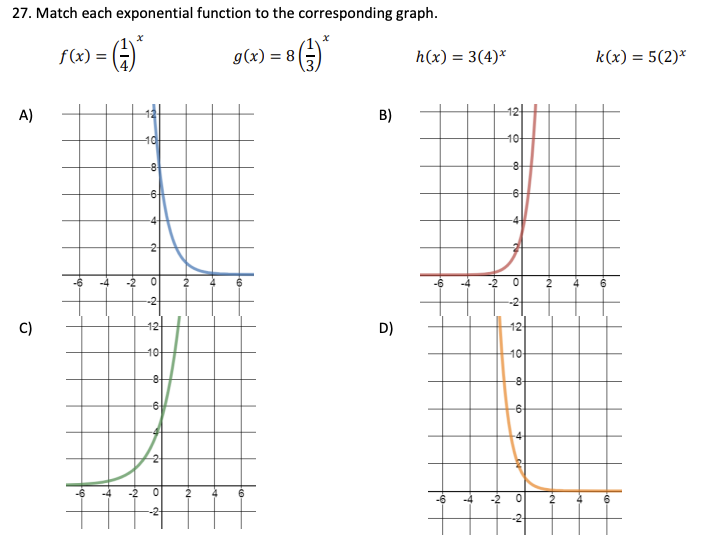
\f4. Simplify each expression into the form a . b*. a. 3*-4(27)*-1 b. 6*+2 +6*Directions: For #20-25, solve each equation for x with a calculator. 20. log4 37 = x 21. 2* + 5 = 30 22. 4ex - 2 = 14 23. 32% = 53x-2 24. 2 In(3x - 1) +4 = 8 25. 32* + 3* -6=026. An exponential function passes through the points (0, 2), (1, 6), and (2, 18). Write the equation that satisfies the conditions.27. Match each exponential function to the corresponding graph. X X f (x) = g(x) = 8 h(x) = 3(4)* k(x) = 5(2)* A) B) 12 10 10 -2 2 -6 -2 2 4 6 C) D) FG 10 10 do 6 -6 4 -2 -N- o31. For a function y = nek , y is the ending amount, n is the initial amount, k is the growth rate, and t is time in hours. A certain culture of bacteria will grow from 500 to 4000 in 1.5 hours. Find the constant k for the growth formula. 32. The half-life of a certain radioactive substance is 14 days. There are 6.6 grams present initially, when will there be 1 gram remaining? 33. The number of students infected with the flu at Springfield Elementary School is observed by Lisa. The equation P(t) represents the number of students infected after t days. 800 P(t) = 1+ 49e-0.2t a. What was the initial number of students infected? b. When will the number of infected students reach 200? c. The school will close when 50% of the student body are infected. When will the school close?34. The management of a factory has found that the maximum number of units a worker can produce in a day is 30. The learning curve for the number of units N produced per day after a new employee has worked t days is given by N(t) = 300(1 - ekt). After 20 days on the job, a worker produces 19 units per day. a. Find the learning curve for this worker. (What is the value of k)? b. How many days should pass before this worker is producing 25 units per day? 35. Find the inverse of each function and state the domain and range for the function and its inverse. a. y = 4(3)3x-1 + 5 b. f (x) = (In(5x - 3) - 1)1/2