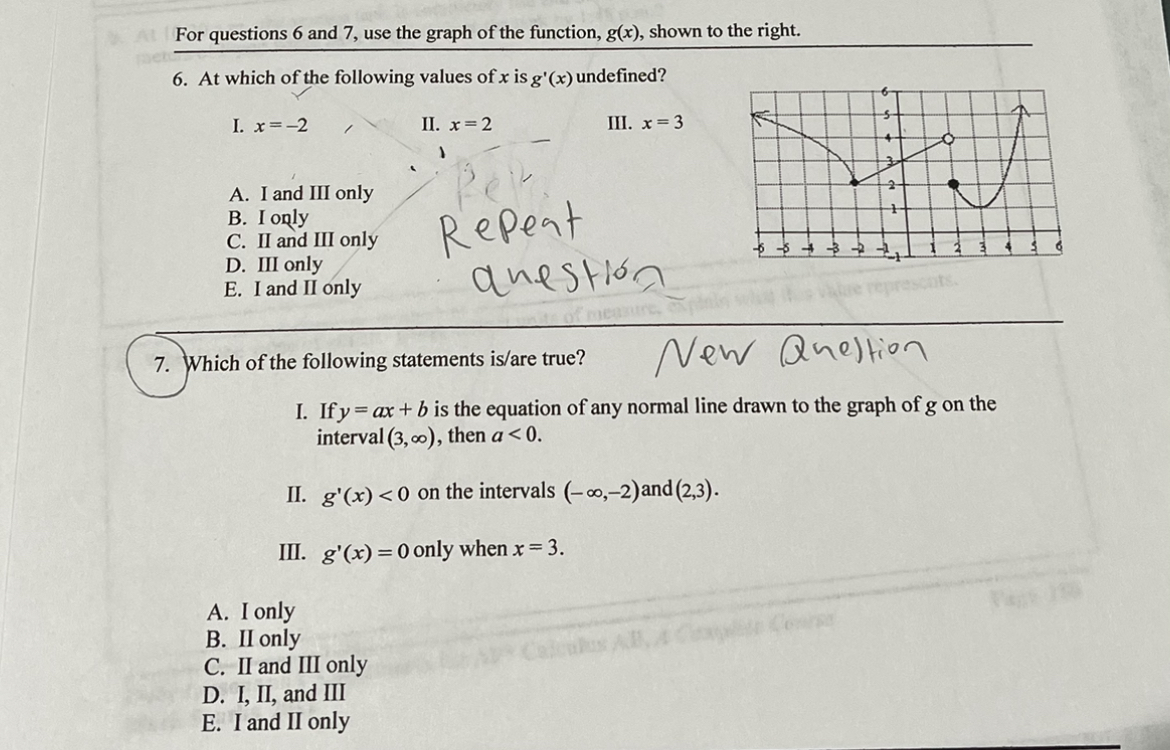
Answer key is attached, I just need help with showing the work. Please show work with justification, box the final answer, and write neatly. Thank you for your support. There may be some repeat problems, If there are please just write repeat problem next to it. This is a study guide to help me study, not being used for any other reasons. All information posted is straight from the review packet. Please do not flag for honor code violation, I am genuinely using this to study.

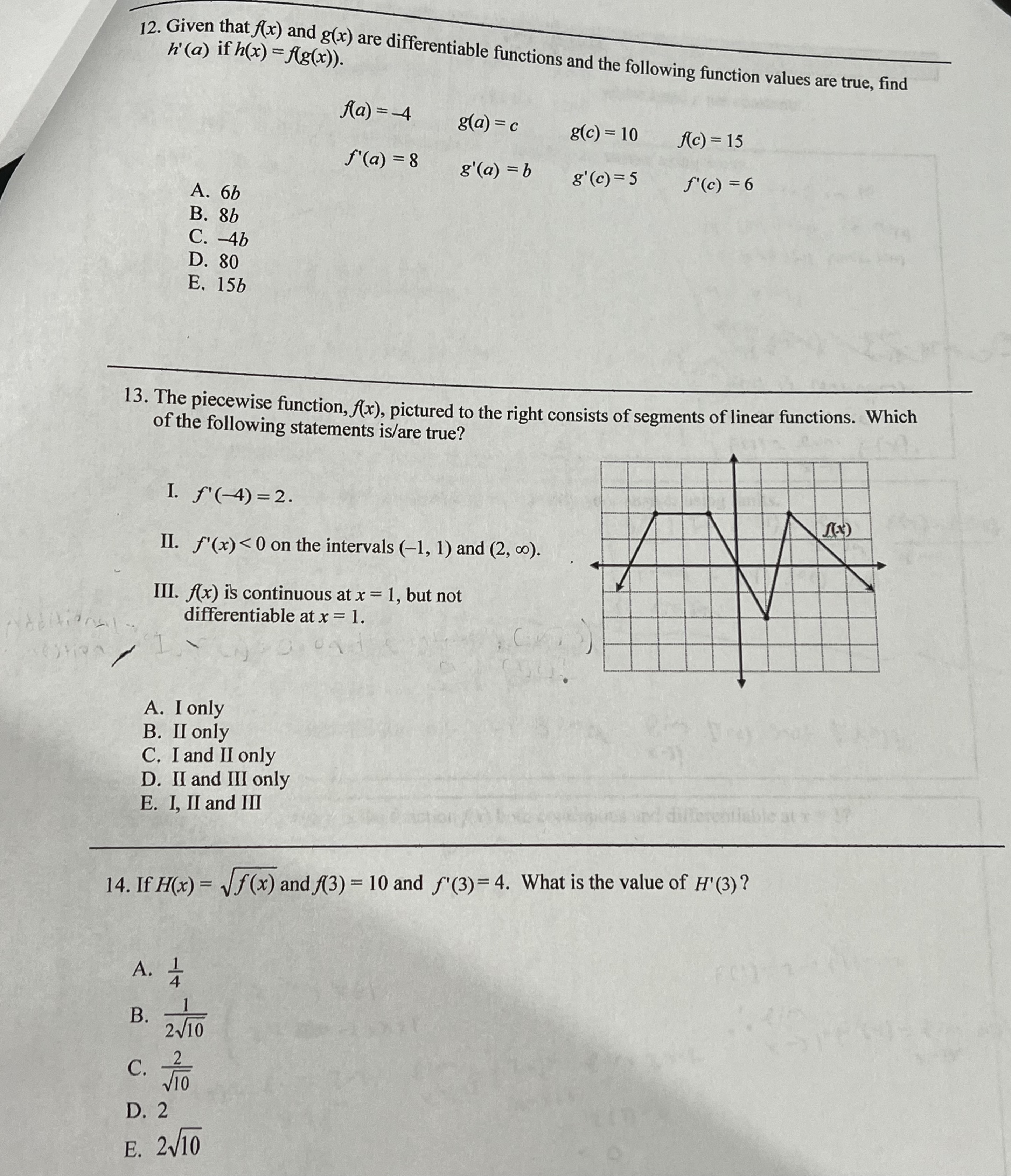
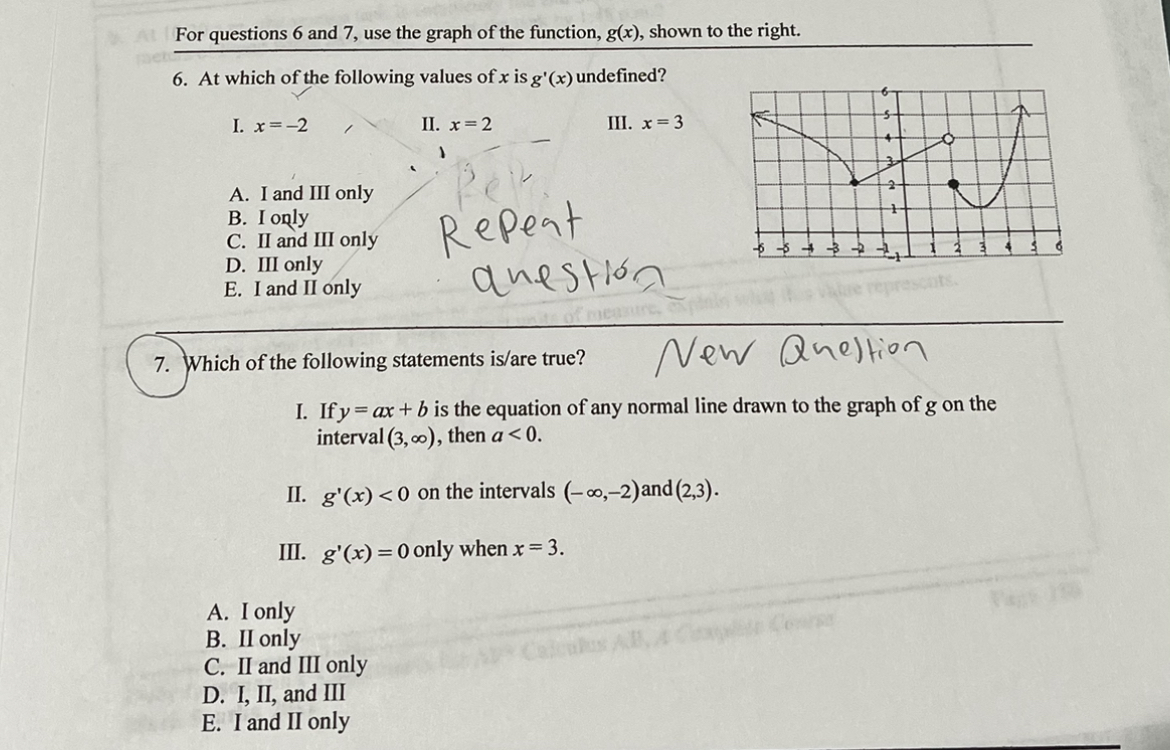
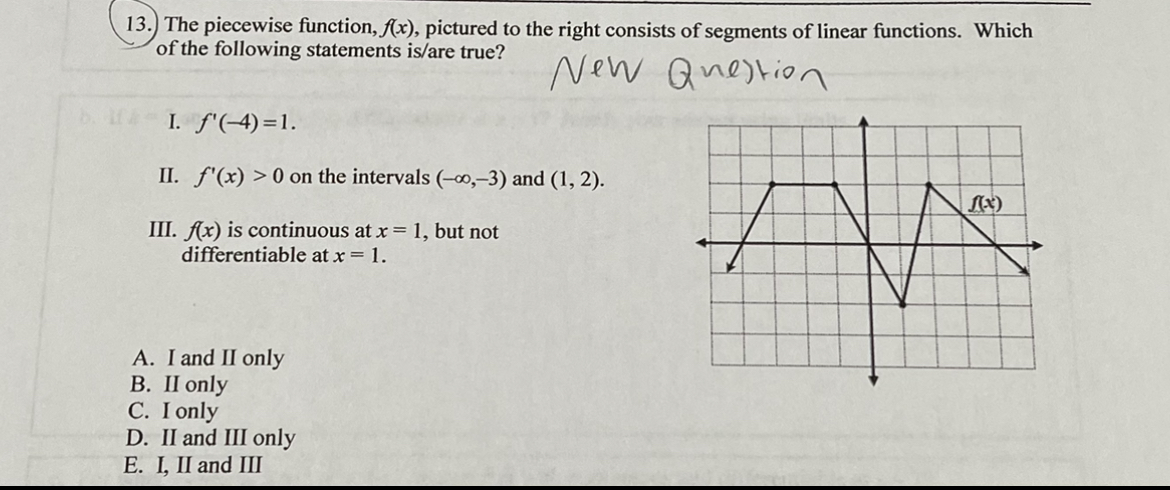
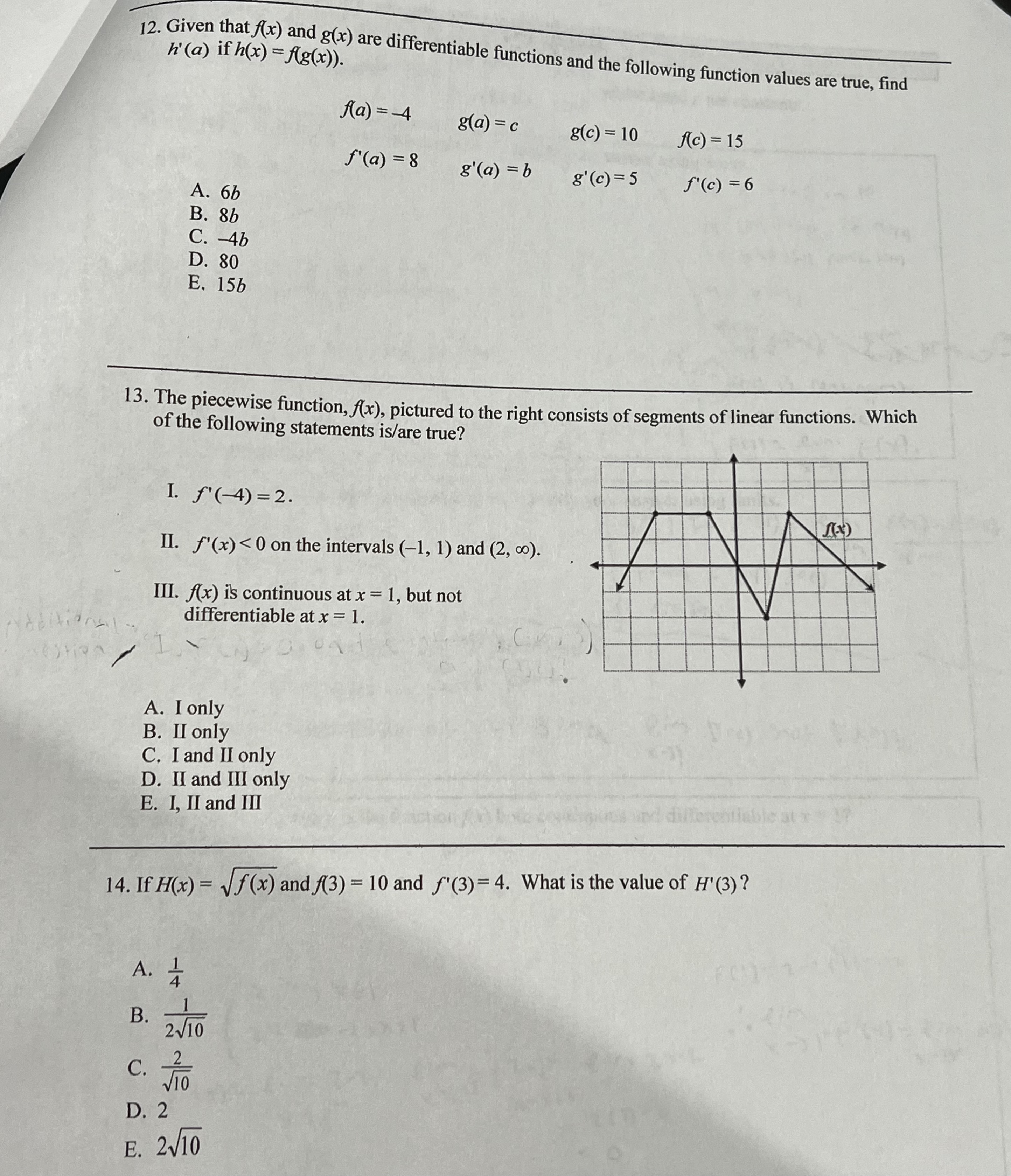
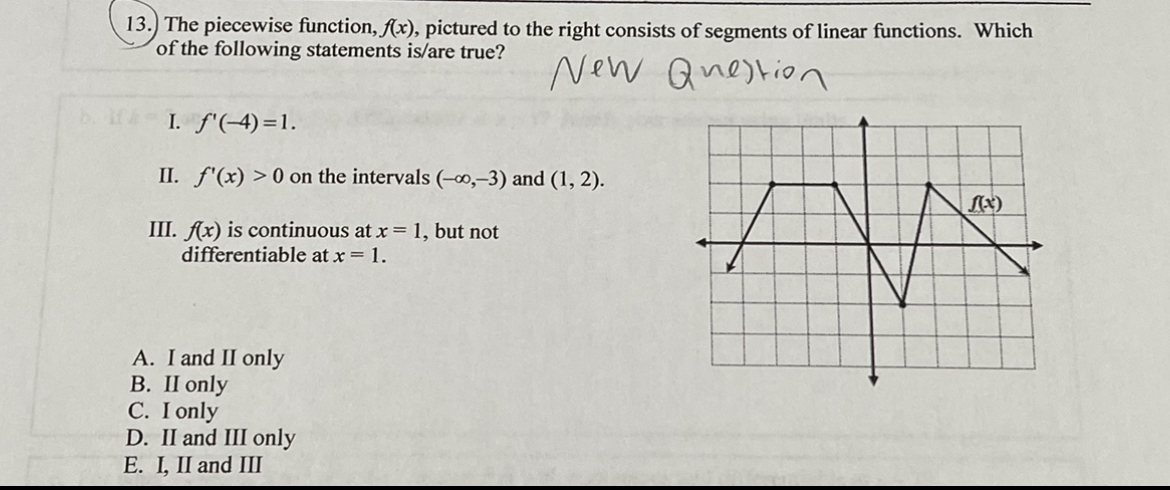
Multiple Choice 16 - Calculator Permitted Calculator Not Permitted 15 - 15.9 90% 13 - 14.9 85% * * - 12.9 80% 1 . 2 . 9 - 10.9 75% 3 . EWODDE 7 - 8.9 70% 4. A C 5. D 5-6.9 65% 6. D 6 . 0 - 4.9* 60% 7 . (With serious attempt) Calculator Permitted Free Response Part A - 2 points total 1 Correctly finds d(t) = 0 when t = 12 meters by either setting the equation equal to 0 and solving algebraically or by looking at the graph or table of values on the graphing calculator. 1 The tank will be completely empty by 6:30 a.m. Calculator Permitted Free Response Part B - 2 points total 1 Finds the value of d(3.25) = 6(1 - 3.25} 12 =3.190 1 Finds the value of the value of d(0) - 6(1-)" =6, which is the initial depth of the water and finds that at 1:45, the depth of the water in the tank is d(0) - d(3.25) = 2.810 meters Calculator Permitted Free Response Part C - 2 points total 1 Correctly finds d'(2) = -0.833 meters per hour 1 d'(2) represents the rate at which the depth of the liquid waste is decreasing 2 hours after the drainage valve is opened. Calculator Permitted Free Response Part D -3 points total 1 Correctly finds d'(0.5) = -0.958 meters per hour 1 Compares d'(2) = -0.833 and d'(0.5) = -0.958 to determine that water is draining out of the tank faster after 30 minutes 1 Justification: Since d'(0.5) is "more negative" than d'(2) , the water is draining faster when t = 0.5. [DO NOT award point if student says d'(0.5)> d'(2) .]\f-2 9. If y = find dy 2x5 at x = 1. dx A. -28 B. -13 C. -52 D. 13 E. 52 Which 10. If the line x + 7y = 29 is an equation of the normal line to the graph of f(x) at the point (1, 4), then what is the value of f' (1) ? A. - 7 B. C. - 1 D. 7 E. -7 1 1. The jim tan 3(x +h) -tan 3x is What is the whe of wop h-0 h A. 0 B. sec (3x) C. 3 sec-(3x) D. 3cot (3x) E. nonexistent12. Given that f(x) and g(x) are differentiable functions and the following function values are true, find h(a) if h(x) = Ag(x)). fa) = -4 g(a) = c g(c) = 10 A(c) = 15 f'(a ) =8 8'(a ) = b 8'(c) = 5 f' ( c ) = 6 A. 6b B. 8b C. -4b D. 80 E. 156 13. The piecewise function, f(x), pictured to the right consists of segments of linear functions. Which of the following statements is/are true? I. f' (-4) = 2. II. f'(x) 0 on the intervals (-co,-3) and (1, 2). III. A(x) is continuous at x = 1, but not differentiable at x = 1. A. I and II only B. II only C. I only D. II and III only E. I, II and