ANSWER ONLY

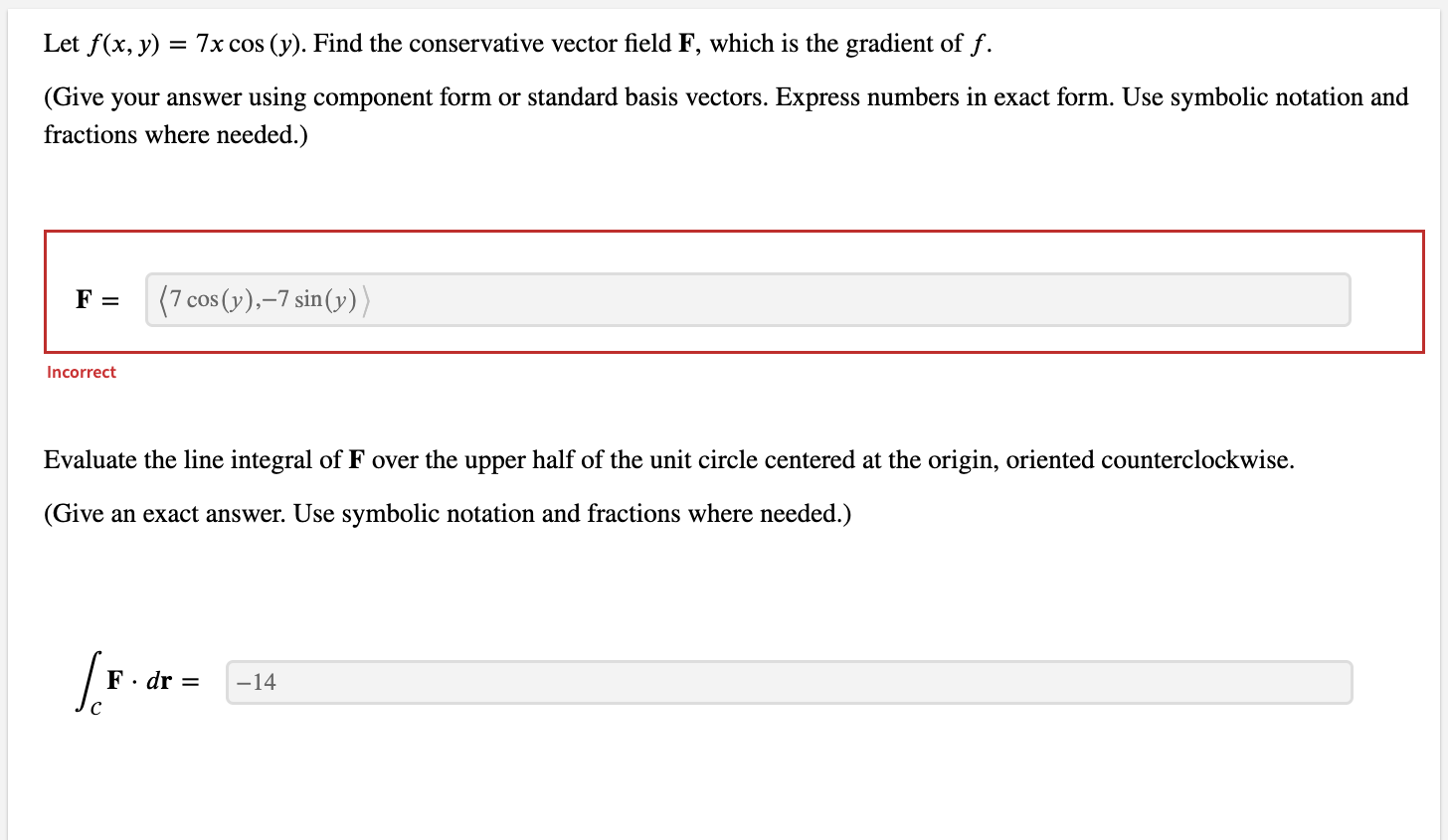
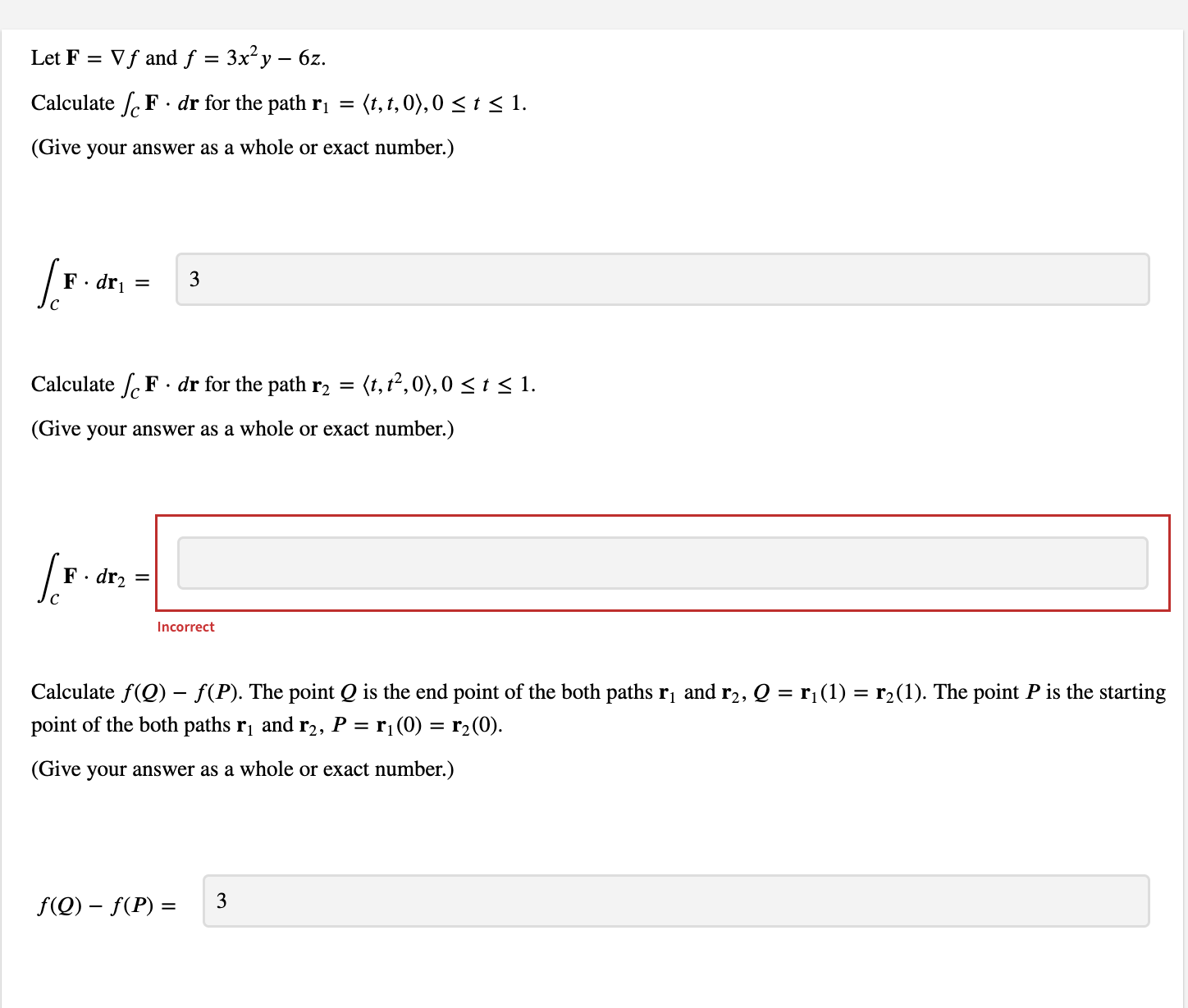
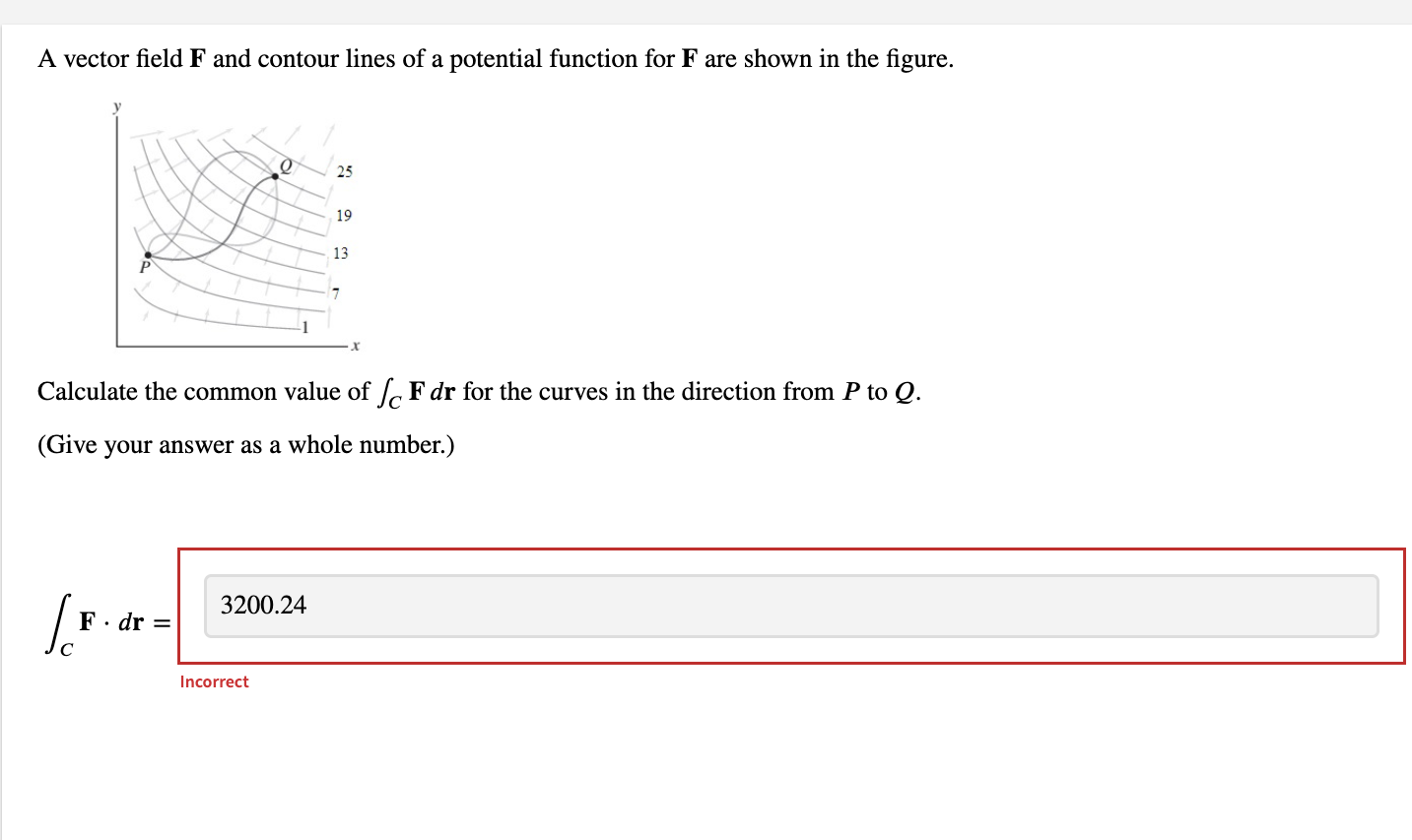
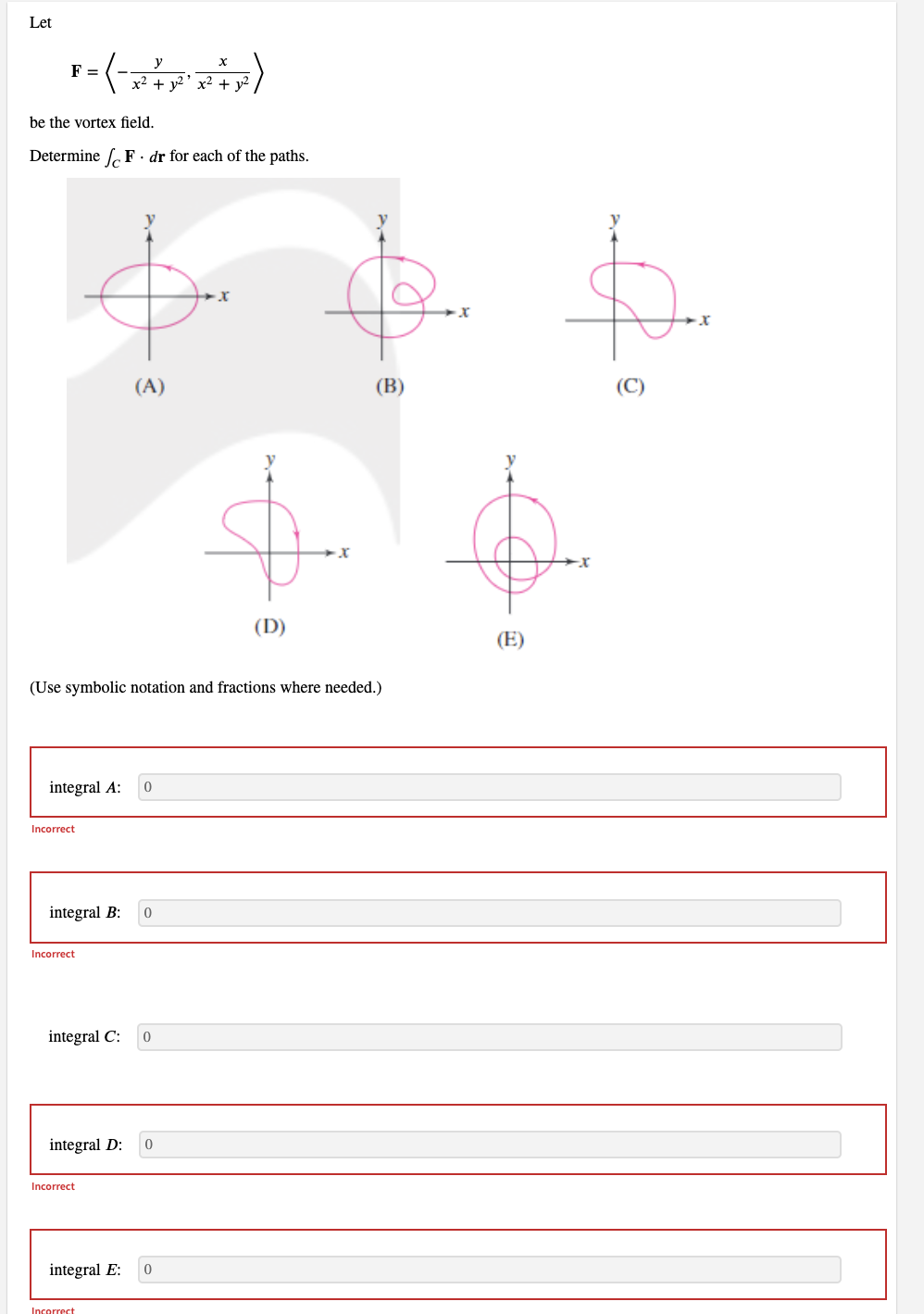
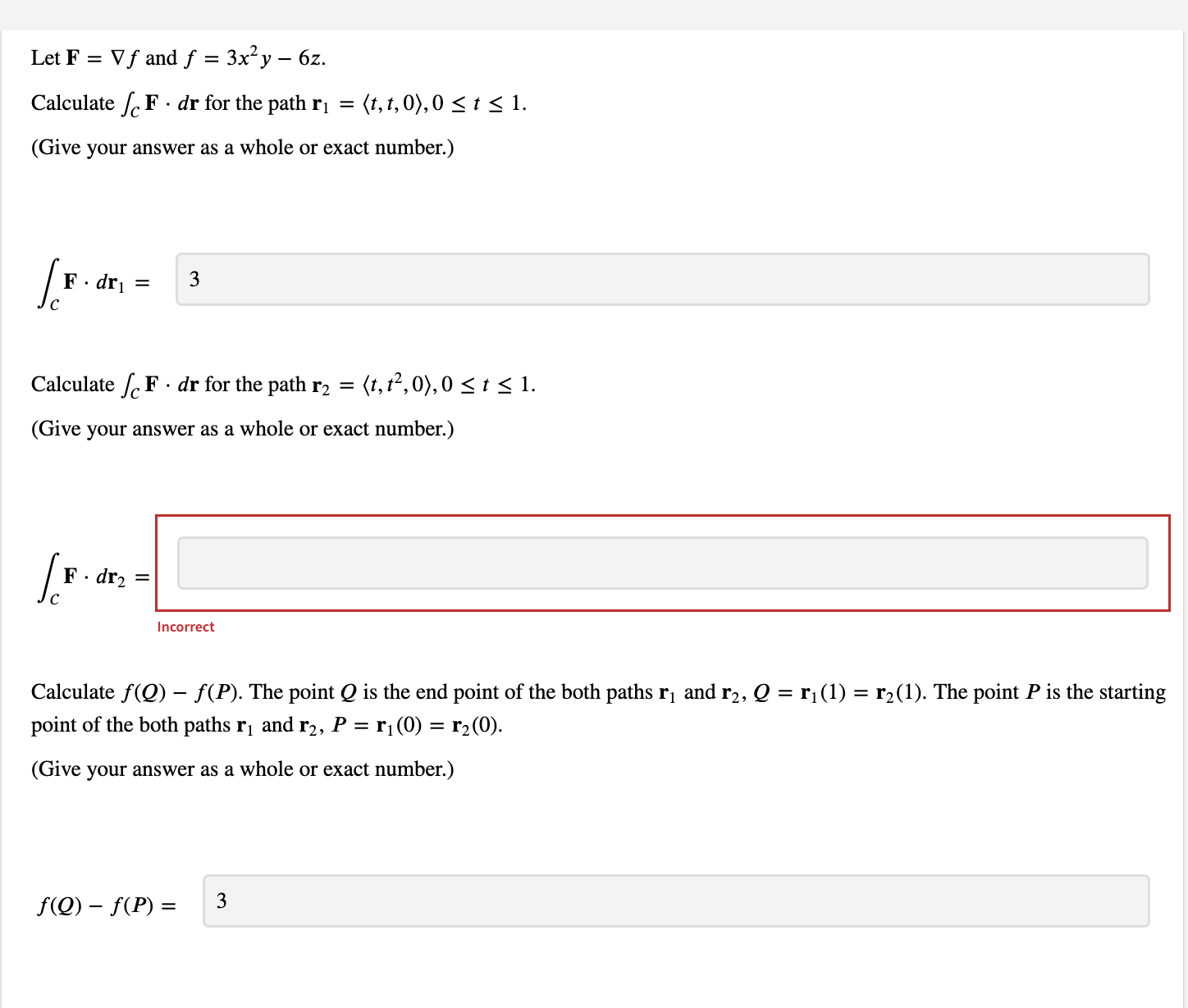
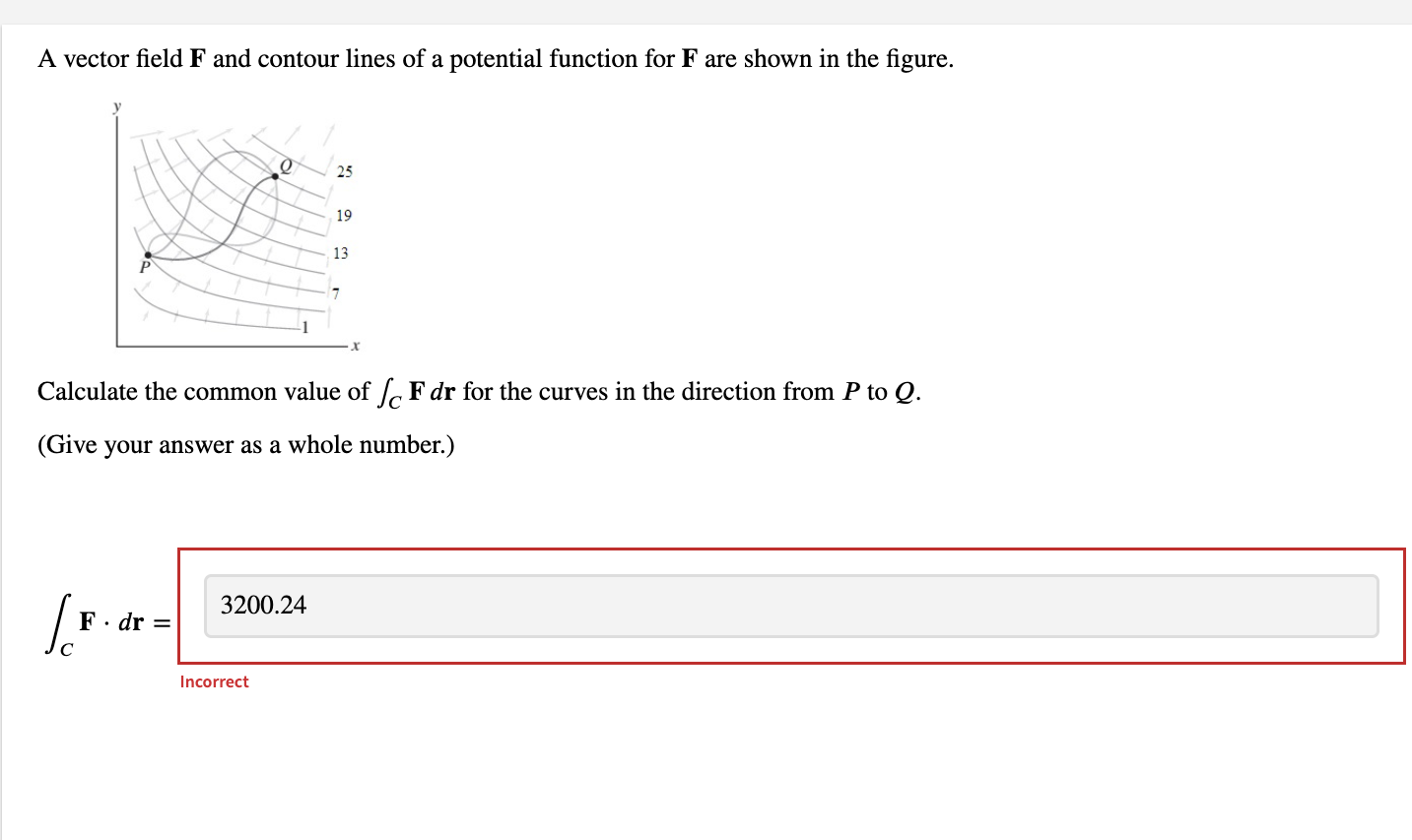
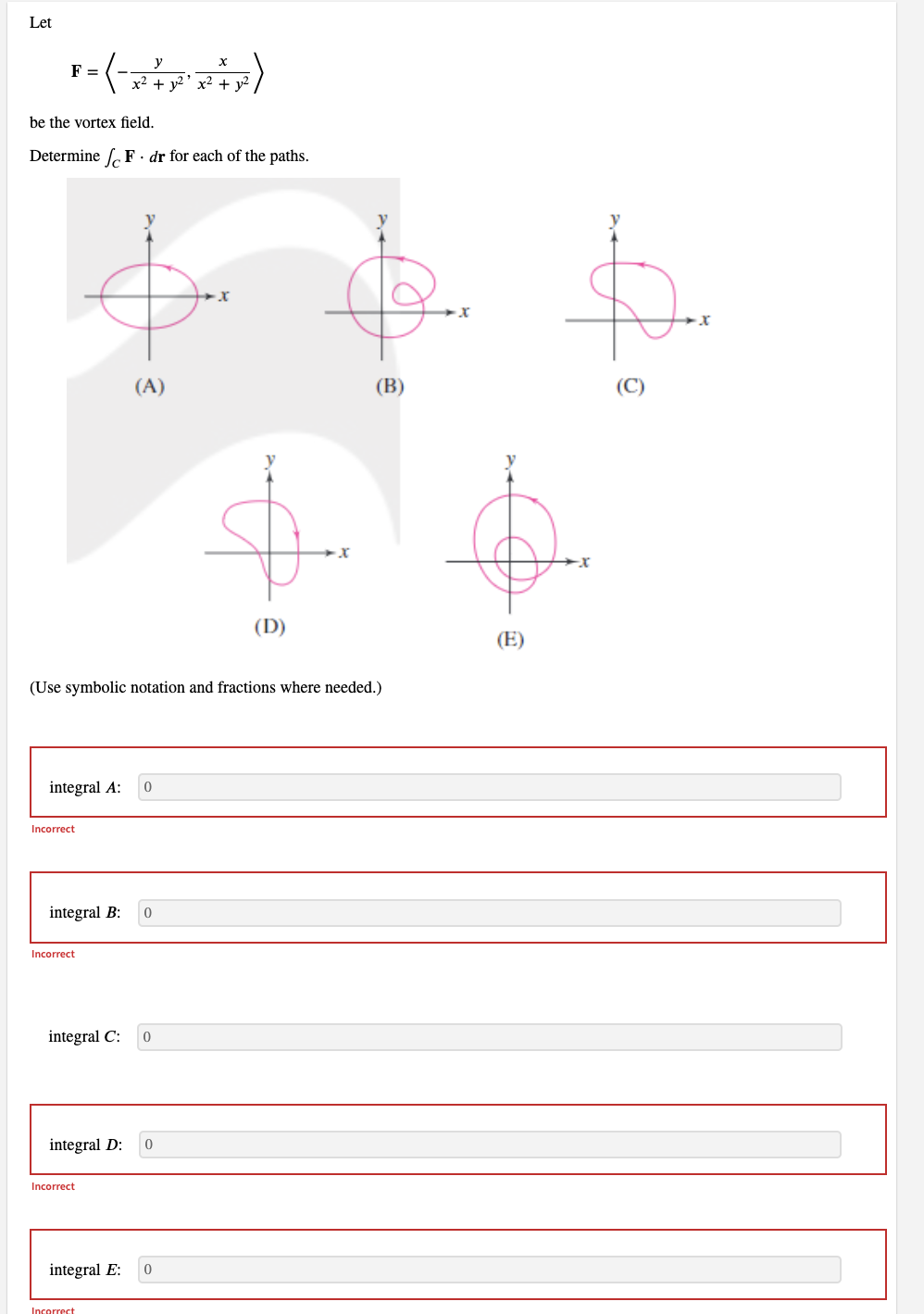
Let f(x, y, z) = 6xy sin (yz) and F = Vf. Evaluate / F . dr, where C is any path from (0, 0, 0) to (5, 1, IT). (Use symbolic notation and fractions where needed.) F . dr = i + 6j + 6 In(x) k IncorrectLet f(x, y) = 7x cos (y). Find the conservative vector field F, which is the gradient of f. (Give your answer using component form or standard basis vectors. Express numbers in exact form. Use symbolic notation and fractions where needed.) F = (7 cos(y),-7 sin(y) Incorrect Evaluate the line integral of F over the upper half of the unit circle centered at the origin, oriented counterclockwise. (Give an exact answer. Use symbolic notation and fractions where needed.) F . dr = -14Let f(x, y, z) = by + 6z In(x). Find the conservative vector field F, which is the gradient of f. (Use symbolic notation and fractions where needed.) F = Evaluate the line integral of F over the circle (x - 5)2 + y = 1 in the counterclockwise direction. (Use symbolic notation and fractions where needed.) F . dr =Let F = Vf and f = 3x y - 6z. Calculate S F . dr for the path r1 = (t, t, 0), 0