Answer plz on this I will give you upvote

Answer plz on this I will give you upvote

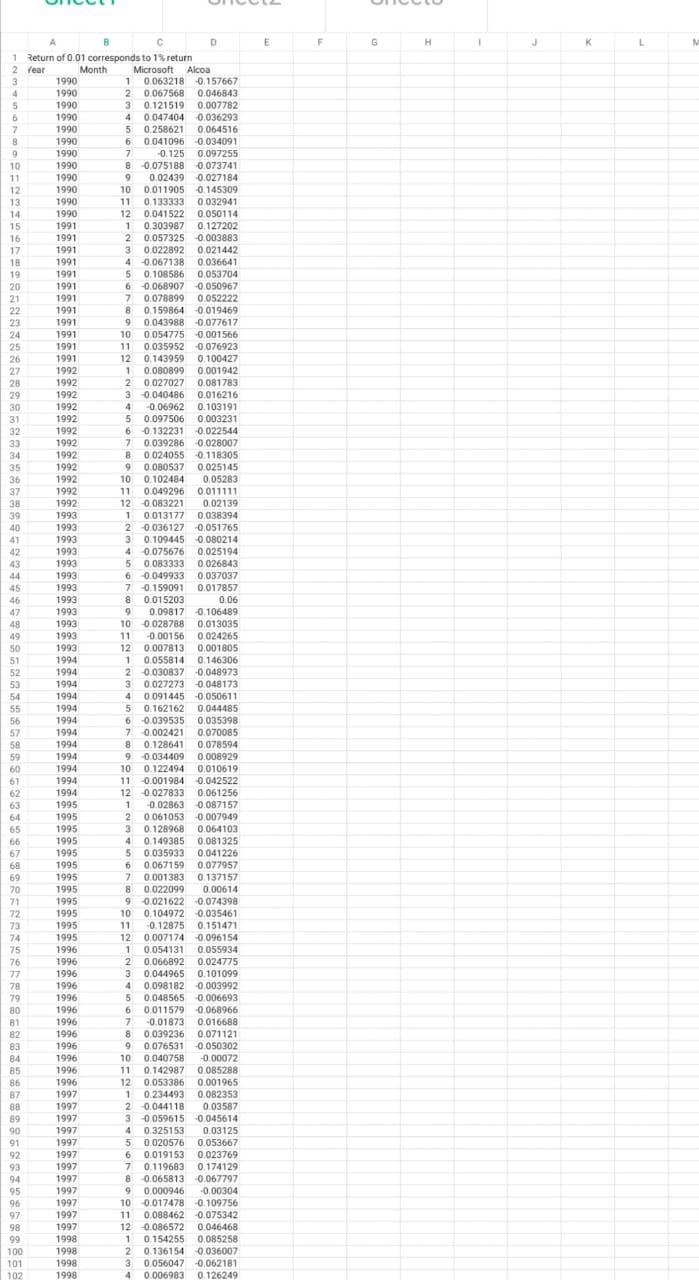
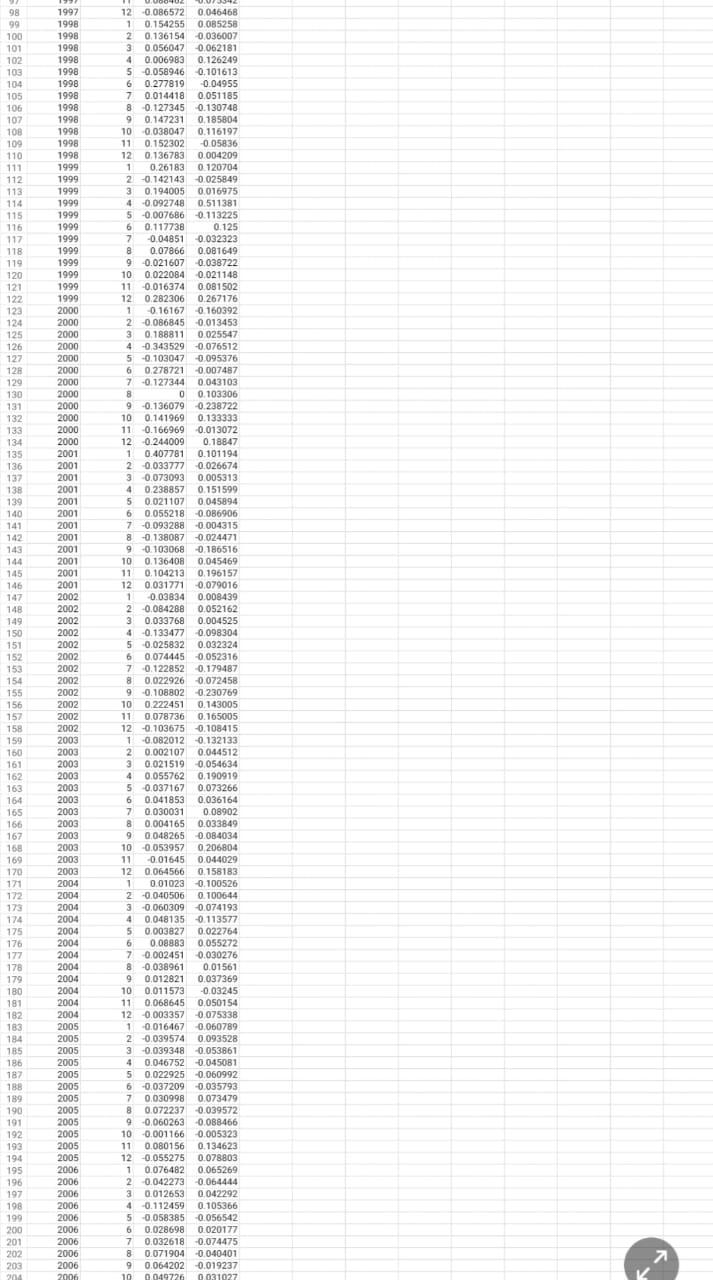
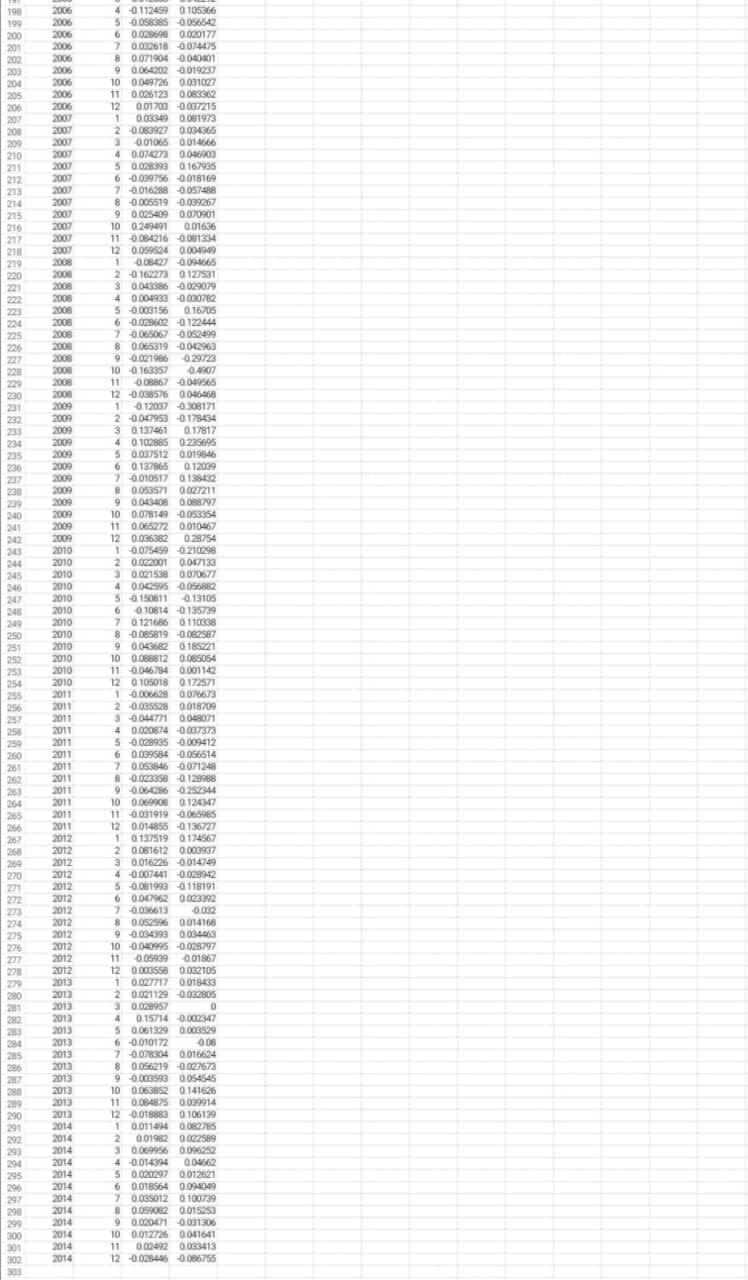
Problem 8: Portfolio Choice Using Numerical Methods (6 points) For this problem, you will need data in Excel file homework3.data.2.xlsx available on Black- board, which contains monthly returns on Microsoft and Alcoa stocks. Assume that those are only 2 stocks on the market. You will need to use a statistical software. Microsoft Excel should satisfy your needs, but you can use anything else you prefer. Do all tasks below at monthly frequency. Use population statistics to compute return properties. a) (0.5 point) Compute the expected return and standard deviation of Microsoft. b) (0.5 point) Compute the expected retum and standard deviation of Alcoa. C) (0.5 point) Compute the covariance and correlation between Microsoft and Alcoa returns. d) (1 point) Construct the grid of possible portfolio allocations. Assume that a is the portfolio allocation to Microsoft. Assume that a is between 0 and 1 and use the grid precision of 0.005 (0.5%). Thus, your grid is going to be 0.0.005, 0.01, 0.015.0.985, 0.99, 0.995, 1. For each portfolio allocation on the grid, compute the expected return and the standard deviation using properties of individual assets from a)-c). Do not report the whole grid in the answer: report only the rows corresponding to the following values of a: 0.1,0.3, 0.7 and 0.95. e) (0.5 point) Plot the opportunity set in the standard deviation-expected return domain. Use the grid constructed in part d) to answer the questions below: (1 point) What is the minimum standard deviation you can achieve using those 2 assets? What is (approximately) the portfolio allocation to Microsoft to achieve that standard deviation? g) (1 point) Suppose the maximum monthly standard deviation you can tolerate is 9%. What is your optimal portfolio allocation among Alcoa and Microsoft stocks? h) (1 point) Suppose that the monthly risk-free rate is 0.1% and you can both invest and borrow at this rate. What is the weight of Microsoft in the aggregate market portfolio? E E F G H 1 j K A B D 1 Return of 0.01 corresponds to 1 return 2 Year Month Microsoft Alcoa 1990 10.063218 0.157667 4 1990 20.067568 0.046843 5 1990 30.121519 0.007782 1990 4 0.047404 0.036293 7 1990 5 0.258621 0,064516 B 1990 6 0.041096 0.034091 9 1990 7 -0.125 0.097255 10 1990 B 0.075188 0.073741 11 1990 9 0.02439 0.027184 12 1990 10 0.011905 0.145309 13 1990 11 0.133333 0032941 14 1990 12 0.041522 0.050114 15 1991 1 10.303987 0.127202 16 1991 20.057325 0.003883 17 1991 30022892 0.021442 18 1991 40.067138 0036641 19 1991 5 0.108586 0,053704 20 1991 6 -0.068907 0.050967 21 1991 7 0.078899 0.052222 22 1991 8 0.1598640019469 23 1991 9 0.0439880077617 24 1991 10 0054775 -0.001566 25 1991 11 0.035952 0.076923 26 1991 12 0.143959 0.100427 27 1992 1 0.080899 0.001942 28 1992 20.027027 0.081783 29 1992 30.040466 0.016216 30 1992 4 -0.06962 0.103191 31 1992 5 0.097506 0.003231 32 1992 60.132231 0.022544 33 1992 7 0.039286 0.028007 34 1992 800240550118305 35 1992 90.000537 0.025145 36 1992 10 0.102484 0.05283 37 1992 11 0.049296 0.011111 38 1992 120083221 0.02139 39 1993 1 0.013177 0.038394 40 1993 2 0.036127 0,051765 41 1993 30.109445 0.080214 42 1993 4 0.075676 0.025194 43 1993 50.083333 0.026843 44 1993 6 0.049933 0.037037 45 1993 70.159091 0.017857 46 1993 8 0.015203 0.06 47 1993 9 9 0.098170.106489 48 1993 10 0.028788 0,013035 49 1993 11 -0.00156 0.024265 50 1993 12 0.007813 0.001805 51 1994 1 0.055814 0.146306 52 1994 20.030837 0.048973 53 1994 0.027273 0.048173 54 1994 4 0.0914450050611 55 1994 5 0.162162 0.044485 56 1994 6 0.039535 0.035398 57 1994 7 0.002421 0.070085 58 1994 80.128641 0.078594 59 1994 9 0.034409 0.008929 60 1994 10 0.122494 0.010619 67 1994 11 0.001984 0.042522 62 1994 12 -0.027833 0.061256 63 1995 1 0.02863 0.087157 1995 20061053 0.007949 65 1995 0.128968 0.064103 66 1995 4 0.149385 0.081325 67 1995 5 0.035933 0.041226 68 1995 6 0.067159 0.077957 69 1995 7 0.001383 0.137157 70 1995 8 0.022099 0.00614 71 1995 90.0216220.074398 72 1995 10 0.104972 0.035461 73 1995 11 0.12875 0.151471 74 1995 12 0007174 0.096154 75 1996 1 0.054131 0.055934 76 1996 2 0.066892 0.024775 77 1996 3 0.044965 0.101099 78 1996 4 0.0981820.003992 79 1996 5 0.048565 0.006693 80 1996 6 0.0115790068966 81 1996 7 -0.01873 0.016688 82 1996 8 0.039236 0,071121 83 1996 90.076531 0.050302 84 1996 10 0.040758 -0.00072 85 1996 11 0.142987 0085288 86 1996 12 0.053386 0.001965 87 1997 1 0.234493 0.002353 88 1997 20.044118 0.03587 89 1997 30059615 0.045614 90 1997 4 0.325153 0.03125 91 1997 5 0.020576 0.053667 92 1997 6 0.019153 0.023769 93 1997 7 0.119683 0.174129 94 1997 8 0,065813 0,067797 95 1997 9 0.000946 -0.00304 96 1997 10 0.017478 0.109756 97 1997 11 0.0884620.075342 98 1997 -0.086572 0.046468 99 1998 1 0.154255 0,085258 100 1998 2 0.136154 0.036007 101 1998 30.056047 0,062181 102 1998 4 0.0069830126249 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 154 165 166 167 155 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 183 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 1997 1998 1998 1998 1998 1998 1998 1998 1998 1998 1998 1998 1998 1999 1999 1999 1999 1999 1999 1999 1999 1999 1999 1999 1999 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2001 2001 2001 2001 2001 2001 2001 2001 2001 2001 2001 2001 2002 2002 2002 2002 2002 2002 2002 2002 2002 2002 2002 2002 2003 2003 2003 2003 2003 2003 2003 2003 2003 2003 2003 2003 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2005 2005 2005 2005 2005 2005 2005 2005 2005 2005 2005 2005 2006 12 0.086572 0.046468 1 0.154255 0.085258 20.136154 0.036007 30.056047 0.062181 4 0.006983 0.126249 5 -0.058946 0.101613 6 0.277819 -0.04955 7 0.014418 0.051185 80.127345 0.130748 9 0.147231 0.185804 10 0.038047 0.116197 11 0.152302 -0.05836 12 0.136783 0.004209 1 0.26183 0120704 2 -0.142143 0.025849 30.194005 0,016975 4 0.092748 0.511381 5 -0.007686 -0.113225 6 0.117738 0.125 7 -0.04851 0.032323 0.07866 0.081649 90.021607 0.038722 100,022084 0.021148 11 -0.016374 0.081502 120.282306 0.267176 1 -0.16167 0.160392 2 -0.086845 0.013453 30.188811 0.025547 -0,343529 -0.076512 5 -0.103047 0.095376 6 0.2787210.007487 7 -0.127344 0 043103 8 0 0 0.103306 9 90.1360790.238722 10 0.141969 0.133333 11 -0.166969 0.013072 12 0.244009 0.18847 1 10.407781 0.101194 20.033777 0.026674 30.073093 0.005313 4 0.238857 0.151599 5 0.021107 0045894 6 0.055218 -0.036906 7 -0.093288 -0.004315 8 8 0138087 -0.024471 9 -0.103068 -0.186516 10 0.136408 0.045469 11 0.104213 0.196157 12 0.031771 0.079016 1 -0.03834 0.008439 20.084288 0.052162 3 0.033768 0.004525 -0.133477 0.098304 5 0.025832 0.032324 6 0.074445 0.052316 70.1228520.179487 8 0.022926 0.072458 90.108802 -0.230769 10 0.222451 0.143005 11 0.078736 0.165005 12 -0.103675 -0.108415 1 -0.082012 0.132133 2 0.002107 0.044512 3 0.0215190054634 4 0.055762 0.190919 5 0.037167 0.073266 6 0.041853 0.036164 7 0.030031 0.08902 8 0,004165 0.033849 9 0,0482650.084034 10 -0.053957 0.206804 11 -0.01645 0.044029 12 0.0645660.158183 1 0.01023 -0.100526 2 -0,040506 0.100644 3 -0.060309 0,074193 4 0.048135 -0.113577 5 0.003827 0.022764 6 0.08983 0.055272 7 0.002451 -0.030276 8 -0.038961 0.01561 9 0.012821 0.037369 100.011573 -0.03245 11 0.068645 0,050154 12 0.003357 -0.075338 1 0.016467 0.060789 20.039574 0.093528 30.039348 -0.053861 4 0.046752 0.045081 5 0.022925 0.060992 6 -0.037209 -0.035793 7 0.030998 0.073479 8 8 0.072237 -0.039572 9 -0,060263 -0.088466 100.001166 0.005323 11 0.080156 0.134623 12 0.055275 0.078803 1 0.076482 0.065269 20.042273 0.064444 30.012653 0.042292 40.112459 0.105366 5 0,058385 -0.056542 6 0.028698 0020177 7 0.032618 -0.074475 8 0.071904 -0.040401 9 9 0.064202 -0.019237 1000497260031027 2006 2006 2006 2006 2006 2006 2006 2006 2000 2006 2006 2006 2006 2006 2005 198 190 200 200 20 200 204 205 200 20 20 200 210 2006 2000 211 212 213 214 215 210 21 2000 2007 2007 2000 2007 2007 2008 219 220 2008 2008 2008 2008 224 2225 220 2009 224 2009 220 2009 240 241 20 244 24 20 240 4 01124590105366 5 0058 056542 60.008640 0.000177 70.000618 60744.75 8 0.07190 0.000301 9006402019:37 10 0.049725 0.001007 110.025123 00362 12 0.017000037215 1 0033490081973 20.083922 0.034365 3001065 0.014666 4 0.03 0.000000 5 0.03 0.167935 60.0097560.018169 7 -0.016388 -0.057488 80.0055190.009267 9 0.0254090070901 10 0209491 001636 11 0084216 08134 12 0.0594 0.001940 1 00022 0.094665 20162273 0127831 3 0.003586 -0.029079 4 0.004933 -0.030762 5 0.003156 015705 6 0062 -122444 7 0.068067 -0.052499 8 0.065319 -0.012963 9 0.007986 029723 100163357 04207 11 0886700565 12 -0.038576 0046468 1012037 0308171 2 -0.027953 -0178434 30.137461 017817 4 0.102885 235695 50.007512 0.019646 6 0.137865 0.12009 0.01051013432 8 0.053571 0027211 90.003409008797 10 0.078149 0.053354 11 0.065272 0.010467 12 0.006382 028754 1 0.075499 0210298 20.06.2001 0.067133 0.021538 070677 4 0.0005 0.050882 50150811 213103 6 0.10814 -135739 7 0.127686 011008 8 -0.085819 -0.062587 9 0.063682 0185221 10 00888120.085054 11 6046754 0.001142 12 0105018 0172571 1 0.006629 0176673 20.005528 0.015709 3 00447710048071 4 0.020824 -0.007373 5 0.028935 009412 6 0.039584 0.056514 70.0535460071248 8 -0.023358 9129988 9 0.06.06 0.357346 10 0.06 0120347 11 0.001919 06965 12 0.014855 0136727 1 0137519 0124567 20.087612 0.003937 30.0162260014749 4 -0.007441 0.029942 5 0.019930118101 6 0.009620023342 70.000613 0.002 8 0.05250014168 9 0.034393 0.03401 10004995 0.028797 11 05939 001867 12 0.000558 0.032105 10.027717 0018433 20.021129 0.032805 300295 0 4 0.15714 0.002347 50061329 0.000529 6 -0.010172 0.08 7 0.072304 0.016624 8 0.056219 0.027673 9 -0.0009230054545 100.163852 0.141626 11 0.084.25 0.029914 12 0.0138830 106139 10.0110100MES 2 0.019520022589 30069956 00922 4 0.014394 00462 5 0.022297 001221 6 0.016564 0.094049 7 0.005012 0190739 80088062 0.015253 9 0.00001 0.031306 10 0.0127260011641 11 0000220033413 12 0.04 0.066755 IS 50 25 256 25 260 25 M4 2 2009 2009 2009 2009 2009 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 2011 2011 2011 2011 2011 2011 2011 2011 2011 2011 2011 2011 2012 2012 2012 2012 2012 2012 2012 2012 2012 2012 2012 2012 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 2014 2014 2014 2014 2014 2014 2014 2014 2014 2014 2014 2014 268 20 220 27 274 235 2 280 29 29 291 29 20 291 29 24 295 290 290 200 100 Problem 8: Portfolio Choice Using Numerical Methods (6 points) For this problem, you will need data in Excel file homework3.data.2.xlsx available on Black- board, which contains monthly returns on Microsoft and Alcoa stocks. Assume that those are only 2 stocks on the market. You will need to use a statistical software. Microsoft Excel should satisfy your needs, but you can use anything else you prefer. Do all tasks below at monthly frequency. Use population statistics to compute return properties. a) (0.5 point) Compute the expected return and standard deviation of Microsoft. b) (0.5 point) Compute the expected retum and standard deviation of Alcoa. C) (0.5 point) Compute the covariance and correlation between Microsoft and Alcoa returns. d) (1 point) Construct the grid of possible portfolio allocations. Assume that a is the portfolio allocation to Microsoft. Assume that a is between 0 and 1 and use the grid precision of 0.005 (0.5%). Thus, your grid is going to be 0.0.005, 0.01, 0.015.0.985, 0.99, 0.995, 1. For each portfolio allocation on the grid, compute the expected return and the standard deviation using properties of individual assets from a)-c). Do not report the whole grid in the answer: report only the rows corresponding to the following values of a: 0.1,0.3, 0.7 and 0.95. e) (0.5 point) Plot the opportunity set in the standard deviation-expected return domain. Use the grid constructed in part d) to answer the questions below: (1 point) What is the minimum standard deviation you can achieve using those 2 assets? What is (approximately) the portfolio allocation to Microsoft to achieve that standard deviation? g) (1 point) Suppose the maximum monthly standard deviation you can tolerate is 9%. What is your optimal portfolio allocation among Alcoa and Microsoft stocks? h) (1 point) Suppose that the monthly risk-free rate is 0.1% and you can both invest and borrow at this rate. What is the weight of Microsoft in the aggregate market portfolio? E E F G H 1 j K A B D 1 Return of 0.01 corresponds to 1 return 2 Year Month Microsoft Alcoa 1990 10.063218 0.157667 4 1990 20.067568 0.046843 5 1990 30.121519 0.007782 1990 4 0.047404 0.036293 7 1990 5 0.258621 0,064516 B 1990 6 0.041096 0.034091 9 1990 7 -0.125 0.097255 10 1990 B 0.075188 0.073741 11 1990 9 0.02439 0.027184 12 1990 10 0.011905 0.145309 13 1990 11 0.133333 0032941 14 1990 12 0.041522 0.050114 15 1991 1 10.303987 0.127202 16 1991 20.057325 0.003883 17 1991 30022892 0.021442 18 1991 40.067138 0036641 19 1991 5 0.108586 0,053704 20 1991 6 -0.068907 0.050967 21 1991 7 0.078899 0.052222 22 1991 8 0.1598640019469 23 1991 9 0.0439880077617 24 1991 10 0054775 -0.001566 25 1991 11 0.035952 0.076923 26 1991 12 0.143959 0.100427 27 1992 1 0.080899 0.001942 28 1992 20.027027 0.081783 29 1992 30.040466 0.016216 30 1992 4 -0.06962 0.103191 31 1992 5 0.097506 0.003231 32 1992 60.132231 0.022544 33 1992 7 0.039286 0.028007 34 1992 800240550118305 35 1992 90.000537 0.025145 36 1992 10 0.102484 0.05283 37 1992 11 0.049296 0.011111 38 1992 120083221 0.02139 39 1993 1 0.013177 0.038394 40 1993 2 0.036127 0,051765 41 1993 30.109445 0.080214 42 1993 4 0.075676 0.025194 43 1993 50.083333 0.026843 44 1993 6 0.049933 0.037037 45 1993 70.159091 0.017857 46 1993 8 0.015203 0.06 47 1993 9 9 0.098170.106489 48 1993 10 0.028788 0,013035 49 1993 11 -0.00156 0.024265 50 1993 12 0.007813 0.001805 51 1994 1 0.055814 0.146306 52 1994 20.030837 0.048973 53 1994 0.027273 0.048173 54 1994 4 0.0914450050611 55 1994 5 0.162162 0.044485 56 1994 6 0.039535 0.035398 57 1994 7 0.002421 0.070085 58 1994 80.128641 0.078594 59 1994 9 0.034409 0.008929 60 1994 10 0.122494 0.010619 67 1994 11 0.001984 0.042522 62 1994 12 -0.027833 0.061256 63 1995 1 0.02863 0.087157 1995 20061053 0.007949 65 1995 0.128968 0.064103 66 1995 4 0.149385 0.081325 67 1995 5 0.035933 0.041226 68 1995 6 0.067159 0.077957 69 1995 7 0.001383 0.137157 70 1995 8 0.022099 0.00614 71 1995 90.0216220.074398 72 1995 10 0.104972 0.035461 73 1995 11 0.12875 0.151471 74 1995 12 0007174 0.096154 75 1996 1 0.054131 0.055934 76 1996 2 0.066892 0.024775 77 1996 3 0.044965 0.101099 78 1996 4 0.0981820.003992 79 1996 5 0.048565 0.006693 80 1996 6 0.0115790068966 81 1996 7 -0.01873 0.016688 82 1996 8 0.039236 0,071121 83 1996 90.076531 0.050302 84 1996 10 0.040758 -0.00072 85 1996 11 0.142987 0085288 86 1996 12 0.053386 0.001965 87 1997 1 0.234493 0.002353 88 1997 20.044118 0.03587 89 1997 30059615 0.045614 90 1997 4 0.325153 0.03125 91 1997 5 0.020576 0.053667 92 1997 6 0.019153 0.023769 93 1997 7 0.119683 0.174129 94 1997 8 0,065813 0,067797 95 1997 9 0.000946 -0.00304 96 1997 10 0.017478 0.109756 97 1997 11 0.0884620.075342 98 1997 -0.086572 0.046468 99 1998 1 0.154255 0,085258 100 1998 2 0.136154 0.036007 101 1998 30.056047 0,062181 102 1998 4 0.0069830126249 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 154 165 166 167 155 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 183 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 1997 1998 1998 1998 1998 1998 1998 1998 1998 1998 1998 1998 1998 1999 1999 1999 1999 1999 1999 1999 1999 1999 1999 1999 1999 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2001 2001 2001 2001 2001 2001 2001 2001 2001 2001 2001 2001 2002 2002 2002 2002 2002 2002 2002 2002 2002 2002 2002 2002 2003 2003 2003 2003 2003 2003 2003 2003 2003 2003 2003 2003 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2005 2005 2005 2005 2005 2005 2005 2005 2005 2005 2005 2005 2006 12 0.086572 0.046468 1 0.154255 0.085258 20.136154 0.036007 30.056047 0.062181 4 0.006983 0.126249 5 -0.058946 0.101613 6 0.277819 -0.04955 7 0.014418 0.051185 80.127345 0.130748 9 0.147231 0.185804 10 0.038047 0.116197 11 0.152302 -0.05836 12 0.136783 0.004209 1 0.26183 0120704 2 -0.142143 0.025849 30.194005 0,016975 4 0.092748 0.511381 5 -0.007686 -0.113225 6 0.117738 0.125 7 -0.04851 0.032323 0.07866 0.081649 90.021607 0.038722 100,022084 0.021148 11 -0.016374 0.081502 120.282306 0.267176 1 -0.16167 0.160392 2 -0.086845 0.013453 30.188811 0.025547 -0,343529 -0.076512 5 -0.103047 0.095376 6 0.2787210.007487 7 -0.127344 0 043103 8 0 0 0.103306 9 90.1360790.238722 10 0.141969 0.133333 11 -0.166969 0.013072 12 0.244009 0.18847 1 10.407781 0.101194 20.033777 0.026674 30.073093 0.005313 4 0.238857 0.151599 5 0.021107 0045894 6 0.055218 -0.036906 7 -0.093288 -0.004315 8 8 0138087 -0.024471 9 -0.103068 -0.186516 10 0.136408 0.045469 11 0.104213 0.196157 12 0.031771 0.079016 1 -0.03834 0.008439 20.084288 0.052162 3 0.033768 0.004525 -0.133477 0.098304 5 0.025832 0.032324 6 0.074445 0.052316 70.1228520.179487 8 0.022926 0.072458 90.108802 -0.230769 10 0.222451 0.143005 11 0.078736 0.165005 12 -0.103675 -0.108415 1 -0.082012 0.132133 2 0.002107 0.044512 3 0.0215190054634 4 0.055762 0.190919 5 0.037167 0.073266 6 0.041853 0.036164 7 0.030031 0.08902 8 0,004165 0.033849 9 0,0482650.084034 10 -0.053957 0.206804 11 -0.01645 0.044029 12 0.0645660.158183 1 0.01023 -0.100526 2 -0,040506 0.100644 3 -0.060309 0,074193 4 0.048135 -0.113577 5 0.003827 0.022764 6 0.08983 0.055272 7 0.002451 -0.030276 8 -0.038961 0.01561 9 0.012821 0.037369 100.011573 -0.03245 11 0.068645 0,050154 12 0.003357 -0.075338 1 0.016467 0.060789 20.039574 0.093528 30.039348 -0.053861 4 0.046752 0.045081 5 0.022925 0.060992 6 -0.037209 -0.035793 7 0.030998 0.073479 8 8 0.072237 -0.039572 9 -0,060263 -0.088466 100.001166 0.005323 11 0.080156 0.134623 12 0.055275 0.078803 1 0.076482 0.065269 20.042273 0.064444 30.012653 0.042292 40.112459 0.105366 5 0,058385 -0.056542 6 0.028698 0020177 7 0.032618 -0.074475 8 0.071904 -0.040401 9 9 0.064202 -0.019237 1000497260031027 2006 2006 2006 2006 2006 2006 2006 2006 2000 2006 2006 2006 2006 2006 2005 198 190 200 200 20 200 204 205 200 20 20 200 210 2006 2000 211 212 213 214 215 210 21 2000 2007 2007 2000 2007 2007 2008 219 220 2008 2008 2008 2008 224 2225 220 2009 224 2009 220 2009 240 241 20 244 24 20 240 4 01124590105366 5 0058 056542 60.008640 0.000177 70.000618 60744.75 8 0.07190 0.000301 9006402019:37 10 0.049725 0.001007 110.025123 00362 12 0.017000037215 1 0033490081973 20.083922 0.034365 3001065 0.014666 4 0.03 0.000000 5 0.03 0.167935 60.0097560.018169 7 -0.016388 -0.057488 80.0055190.009267 9 0.0254090070901 10 0209491 001636 11 0084216 08134 12 0.0594 0.001940 1 00022 0.094665 20162273 0127831 3 0.003586 -0.029079 4 0.004933 -0.030762 5 0.003156 015705 6 0062 -122444 7 0.068067 -0.052499 8 0.065319 -0.012963 9 0.007986 029723 100163357 04207 11 0886700565 12 -0.038576 0046468 1012037 0308171 2 -0.027953 -0178434 30.137461 017817 4 0.102885 235695 50.007512 0.019646 6 0.137865 0.12009 0.01051013432 8 0.053571 0027211 90.003409008797 10 0.078149 0.053354 11 0.065272 0.010467 12 0.006382 028754 1 0.075499 0210298 20.06.2001 0.067133 0.021538 070677 4 0.0005 0.050882 50150811 213103 6 0.10814 -135739 7 0.127686 011008 8 -0.085819 -0.062587 9 0.063682 0185221 10 00888120.085054 11 6046754 0.001142 12 0105018 0172571 1 0.006629 0176673 20.005528 0.015709 3 00447710048071 4 0.020824 -0.007373 5 0.028935 009412 6 0.039584 0.056514 70.0535460071248 8 -0.023358 9129988 9 0.06.06 0.357346 10 0.06 0120347 11 0.001919 06965 12 0.014855 0136727 1 0137519 0124567 20.087612 0.003937 30.0162260014749 4 -0.007441 0.029942 5 0.019930118101 6 0.009620023342 70.000613 0.002 8 0.05250014168 9 0.034393 0.03401 10004995 0.028797 11 05939 001867 12 0.000558 0.032105 10.027717 0018433 20.021129 0.032805 300295 0 4 0.15714 0.002347 50061329 0.000529 6 -0.010172 0.08 7 0.072304 0.016624 8 0.056219 0.027673 9 -0.0009230054545 100.163852 0.141626 11 0.084.25 0.029914 12 0.0138830 106139 10.0110100MES 2 0.019520022589 30069956 00922 4 0.014394 00462 5 0.022297 001221 6 0.016564 0.094049 7 0.005012 0190739 80088062 0.015253 9 0.00001 0.031306 10 0.0127260011641 11 0000220033413 12 0.04 0.066755 IS 50 25 256 25 260 25 M4 2 2009 2009 2009 2009 2009 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 2011 2011 2011 2011 2011 2011 2011 2011 2011 2011 2011 2011 2012 2012 2012 2012 2012 2012 2012 2012 2012 2012 2012 2012 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 2014 2014 2014 2014 2014 2014 2014 2014 2014 2014 2014 2014 268 20 220 27 274 235 2 280 29 29 291 29 20 291 29 24 295 290 290 200 100