Question: answer quick and correctly!! Question 6 (5 points) In Chapter 1 we discussed the Argument from Disagreement for Moral Relativism. Which of the following statements

answer quick and correctly!! Question 6 (5 answer quick and correctly!!

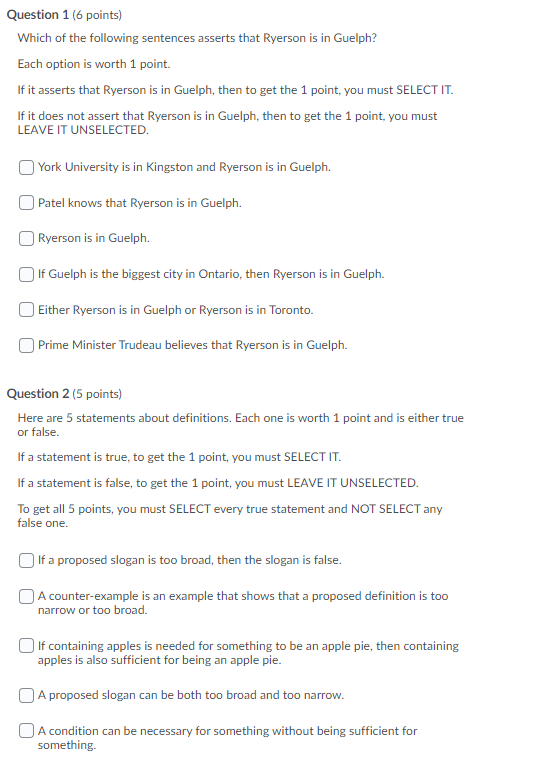
Question 6 (5 points) In Chapter 1 we discussed the Argument from Disagreement for Moral Relativism. Which of the following statements about it are true? Each statement below is worth 1 point and is either true or false. If a statement is true, to get the 1 point, you must SELECT IT. If a statement is false, to get the 1 point, you must LEAVE IT UNSELECTED. To get all 5 points, you must SELECT every true statement and NOT SELECT any false one. Even if the argument's first premise is true, its second premise might be false. The argument is valid The argument's premises are dependent, in the sense we defined in chapter 3. The argument's conclusion is a conditional. Even if the argument is not a good one, the conclusion might still be true. Question 16 points) Which of the following sentences asserts that Ryerson is in Guelph? Each option is worth 1 point. If it asserts that Ryerson is in Guelph, then to get the 1 point, you must SELECT IT. If it does not assert that Ryerson is in Guelph, then to get the 1 point, you must LEAVE IT UNSELECTED. York University is in Kingston and Ryerson is in Guelph. Patel knows that Ryerson is in Guelph. Ryerson is in Guelph. If Guelph is the biggest city in Ontario, then Ryerson is in Guelph. Either Ryerson is in Guelph or Ryerson is in Toronto. Prime Minister Trudeau believes that Ryerson is in Guelph. Question 2 (5 points) Here are 5 statements about definitions. Each one is worth 1 point and is either true or false. If a statement is true, to get the 1 point, you must SELECT IT. If a statement is false, to get the 1 point, you must LEAVE IT UNSELECTED. To get all 5 points, you must SELECT every true statement and NOT SELECT any false one. If a proposed slogan is too broad, then the slogan is false. A counter-example is an example that shows that a proposed definition is too narrow or too broad. If containing apples is needed for something to be an apple pie, then containing apples is also sufficient for being an apple pie. A proposed slogan can be both too broad and too narrow. A condition can be necessary for something without being sufficient for something

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

1. measure of central tendency defining the quantitative average of all raw scores in a data set/sample/population; the sum of raw scores divided by the number of raw scores 2. measure of central...

I need your help. This HM is due tomorrow at 4:00pm Spring 2016 - EBF 304W Homework 2 Due: 5:00pm on Friday, 12 February 2016 (via ANGEL) 50 points Instructions: Please answer all questions clearly...

Please assist with the attached homework. Question 1 (30 Points) On December 31, 2014, Rayco Inc. had the following balances (all balances are normal): Accounts Amount Preferred Stock, ($100 par...

1 (5 points) For a normal distribution with mean of 100 and a standard deviation of 12, find the number of standard deviations the raw score 76 is from the mean. Enter answer as a positive value...

Question 1 (30 Points) On December 31, 2014, Rayco Inc. had the following balances (all balances are normal): Accounts Amount Preferred Stock, ($100 par value, 5% noncumulative, 50,000 shares...

Need a help with journal Question 1 (30 Points) On December 31, 2014, Rayco Inc. had the following balances (all balances are normal): Accounts Amount Preferred Stock, ($100 par value, 5%...

Question 1 (5 points) The following information is taken from a company's records. Applying the lower-of- cost-or-market approach, what is the correct value that should be reported on the balance...

problem 1 -7 need help Question 1 (30 Points) On December 31, 2014, Rayco Inc. had the following balances (all balances are normal): Accounts Amount Preferred Stock, ($100 par value, 5%...

Explain which partitioning strategy is suitable to execute following queries: Q1: The organization wants to improve the manageability of displaying the details of the employees who are working in a...

Suppose you wrote a piece of software that does a better job of allowing computers to network than any other program designed for this purpose. a large networking company wants to incorporate your...

Several investors prefer to have money now rather than later, money received next month instead of later, is not worth as much to those receiving it , assuming the magnitude of the cash flow is...

When older adults have difficulty with transportation and communication, or may be reluctant to request needed assistance to which they are entitled, they may be in need of: Group of answer choices...