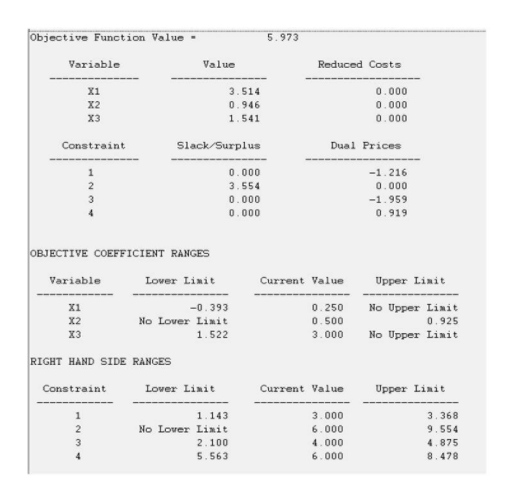
Question: answer the following: No need for solution 35-44: Bluegrass Farm has been experimenting with a special diet for its racehorses. The feed components available for
answer the following: No need for solution





Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


