Answer the question SPECIFIC!

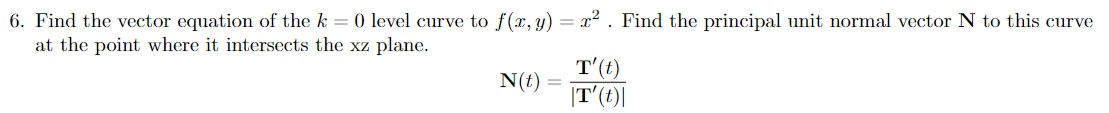
5. Let z = f(:c,y) = e2 Sin(y). a Find the directional derivative of Dgf at the point P0 0, E in direction 1? = G, 8 . 6 (b) What is the maximum value of derivative Darrr, y) at (0, g) (c) At point Pg in what direction would the directional derivative be minimized? (d) If you were walking along the graph of f and reached the point Pa, in what direction would you continue walking so that you experience no elevation loss or gain? 6. Find the vector equation of the k = 0 level mum to f(:1:, y) = 3:2 . Find the principal unit normal vector N to this curve at the point where it intersects the X2 plane. N03) = 7. Let P(1, 0, 1), Q(-2, 1,3) and R(4, 2, 5) be points in R". (a) Find a non zero vector orthogonal to the plane containing the points P, Q, R. (b) Find the area of triangle PQ R.1. Follow the directions below [hint: sketches may be useful]: (a) Describe the surface given by equation: 2 + y + 22 - 62 - 7 = 0 (b) Describe the surface given by equation: y = 0 (c) Find a vector valued function that describes the intersection of the surfaces from (a) and (b) (d) Find the arclength of the intersection described by part (c)