Answer the questions 32, 33, and 34 using the examples given. This is Math for EE and CE.

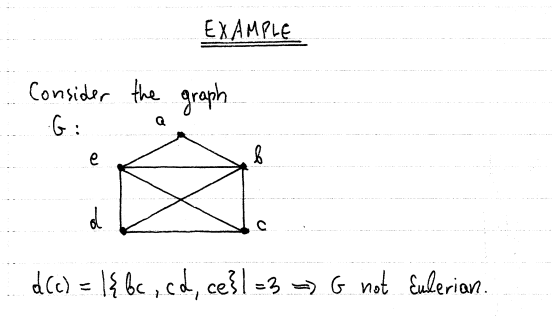
(39) A connected graph with 4 edges and 4 vertices has 2 vertices of degree 2 Show that a) G not Eulerian - 7 Ju E VIG): alul = 3 6 G Eulenan - G regular. 33 Show that a connected regular graph with an odd number of vertices is always Eulerian 34 Show that a connected regular graph with ald number of edges and whose number of vertices is a multiple of 4 is never Eulerian.\fEXAMPLE A connected graph with 5 vertices and 4 edges has two vertices with degree 2. Show that the groph G Is not Eulerian. Solution We assume that IV(6)1 =5 and 1 E ( G)1 = 4 with V ( G) = { U., UQ, 13 , um, US ). and fluid = flue) = 2. Define a = d ( us ) 1 8 = dlugl A c= dlug). From the handshaking lemma: I dlug = 9 /E (Gil => dcultd (ugl+d ( us) +dlug) + dlus) = 2.4 LE VIG) = 2 + 2 + x +6+ c = B - atbic = 4 . 127 G connected - VuEV (G) : dlulz o = a > 1 / by /c> l It follows that atbotc = 4 + ( a , b , c) E g ( 1 , 1 , 2 ), ( 1 , 9, 1), ( 9. 1 1 1)3 and therefore : a odd / b odd Vc odd - => G not Eulerian. B